gilbert strang 교수님의 linear algebra and its applications를 공부하면서 번역과 정리를 해보았습니다.
선형방정식의 기하학을 예제 문제를 통해 이해하도록 하겠습니다.
n=3인 경우(미지수 3개, 방정식 3개)
n=3인 경우를 살펴보겠습니다.

1. row 관점으로 선형방정식을 기하학적으로 표현하기(row picture)
각 방정식은 3차원에서 평면으로 서술할 수 있습니다.
첫 번째 평면은 2u+v+w=5이고 아래 그림처럼 표현할 수 있습니다.
또한 (5/2, 0, 0), (0, 5, 0), (0, 0, 5)를 지나가게 됩니다.

2u+v+w=5에서 5를 10으로 바꾸면 2u+v+w=10이 됩니다.
이는 첫 번째 평면과 평행하게 됩니다.
이처럼 오른쪽 항을 변경하는 것은 평면을 평행 이동하게 합니다.
그리고 2u+v+w=0은 원점을 통과합니다.
두 번째 평면은 4u-6v=-2 입니다.
이것은 수직하게 그려집니다.
w는 어떤 값도 가능하기 때문입니다.
w가 0이지만 3 공간에서 평면으로 남을 수 있습니다.(4u=3, u=0도 동일합니다.)
위 그림에서 두 평면의 교차로는 직선으로 나타내고 있습니다.
3차원에서 직선은 두개의 방정식을 필요로 합니다.
n차원에서 n-1개의 방정식이 필요합니다.
마지막으로 세 번째 평면은 이 직선과 한 점에서 교차합니다.(그림에서 나타나진 않았습니다.)
이 평면을 -2u+7v+2w=9이고 이것은 직선 u=1,v=1,w=2를 교차합니다.
이 세 가지 평면의 교차점(1,1,2)은 선형시스템을 풀 수 있습니다.
어떻게 row picture를 n 차원으로 확장할 수 있을까?
n개의 방정식은 n개의 미지수를 포함합니다.
첫 번째 방정식은 하나의 평면을 결정합니다.
이것은 더이상 3 차원 공간에서 2차원 평면이 아닙니다.
이것은 n-1 차원을 갖게 됩니다.
이것은 n차원 공간에서 매우 얇고 평평하지만 이것은 우리에게 solid하게 보입니다.
만약 4차원으로 보면, t=0 평면이 4차원 공간을 자르고 우리가 살고있는 3차원 세계를 생산합니다.
z=0인 다른 평면 또한 3차원 입니다.
이것은 모든 시간을 빼앗긴 일반적인 x-y 평면입니다.
이 세개의 평면은 교차한 것입니다.
이러한 3차원 평면들은 교차할 것입니다.
그들은 t=0에서 일반적인 x-y 평면을 공유합니다.
2차원으로 내려가서, 다음 평면은 선을 남김니다.
마침내 4번째 평면은 하나의 점을 남깁니다.
이것이 4차원에서 4개의 평면들의 교차로입니다.
이것은 4개의 기초 방정식을 풉니다.
첫번째 방정식은 n차원에서 n-1차원의 평면을 만듭니다.
두번째 평면이 n-1차원의 평면과 교차해 n-2차원 평면을 만듭니다.
이런식으로 매번 새로운 평면(새로운 방정식)은 차원을 하나씩 감소시킵니다.
결국, 교차로는 0차원(점)을 갖게 됩니다.
이 점은 평면위에 놓여있고 점의 좌표는 모든 n개의 방정식을 만족하게 됩니다.
이것이 해(solution) 입니다.
2. 열 벡터들과 선형 결합들 (Column Vectors and Linear Combinations)
이번에는 열(column) 관점에서 방정식을 살펴보겠습니다.

이 방정식을 벡터 방정식(vector equation)으로 표현하면 다음과 같이 됩니다.
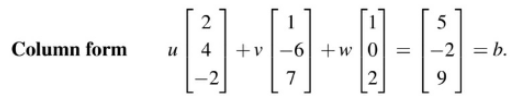
이것은 3차원 열 벡터입니다.
벡터 b는 (5, -2, 9) 좌표를 갖고 있는 점과 동일합니다.
3차원 공간에서 모든 점들은 벡터와 매칭됩니다.
열 벡터를 3가지 방법으로 표현할 수 있습니다.
(1) b = (5, -2, 9)처럼 요소들을 나열하기
(2) 원점으로부터 화살표로 나타내기
(3) 열을 벡터로 표현하기
화살표, 점, 3개의 숫자를 선택할 수 있습니다.
6차원에서는 6개의 숫자를 선택하는 것이 가장 쉽습니다.
요소들을 수평으로 나열할 때 괄호와 콤마가 필요합니다.
수직으로 열벡터를 나타날 때는 (콤마없이) 대괄호가 필요합니다.
가장 중요한 것은 스칼라(숫자)에 의한 곱셈과 벡터의 덧셈입니다.
벡터 덧셈 - Vector addition


세개의 벡터가 더해져 b가 됩니다.
벡터 곱셈 - Multiplication by scalars


선형 결합 - Linear combination
벡터의 곱셈과 덧셈의 결과를 선형 결합(linear combination)이라고 부릅니다.
선형 결합은 방정식을 풀 수 있습니다.

오른쪽 항인 b를 만들기 위해서 u=1, v=1, w=2가 필요합니다.
이는 row picture에서 3개의 평면들의 교차점(1,1,2)로 나타낼 수 있습니다.
n개의 미지의 방정식에는 row picture에서 n개의 평면이 있습니다.
column picture에는 n개의 벡터가 있습니다.
이 방정식들은 b와 동일한 n개 열의 선형 결합을 필요로 합니다.
Row picture : 평면들의 교차점(Intersection of planes)
Column picture : 열들의 결합(Combination of columns)
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 1.2 행 줄임과 사다리꼴 - Row reduction and Echelon forms - 기약 사다리꼴, 선행 성분, 자유 변수, 일반 해, 유일성 (0) | 2020.10.26 |
|---|---|
| [선형대수학] 1.1 선형 방정식계 - Systems of Linear Equations - 소거법, 행 상등, 해의 집합, 행 연산, 행렬 표기법 (0) | 2020.10.26 |
| [선형대수학] ch1-2 선형방정식의 기하학 - 특이한 경우 (0) | 2020.10.24 |
| [선형대수학] ch1.2 선형방정식의 기하학 - n=2일 때 행관점과 열관점 (0) | 2020.10.24 |
| [선형대수학] ch1.1 개요 - Introduction - 소거법과 행렬식과 4가지 핵심내용 (0) | 2020.10.24 |