반응형
gilbert strang 교수님의 linear algebra and its applications를 공부하면서 번역과 정리를 해보았습니다.
1.2 선형방정식의 기하학 - The Geometry of Linear Equations
선형방정식의 기하학을 이해하기 위한 방법으로 예시를 보겠습니다.

이 방정식을 rows와 columns 두 가지 관점에서 볼 수 있습니다.
1. 행(rows) 관점으로 접근
위 방정식은 2차원에 간단하게 표시할 수 있습니다.
2x - y = 1를 x-y평면에서 직선으로 표시됩니다.
이 직선은 (x=1, y=1), (x=1/2, y=0), (x=2, y=3)을 지나갑니다.
x + y = 5는 기울기가 -1인 직선이며 이 직선은 첫번째 직선과 해(solution)에서 교차하게 됩니다.
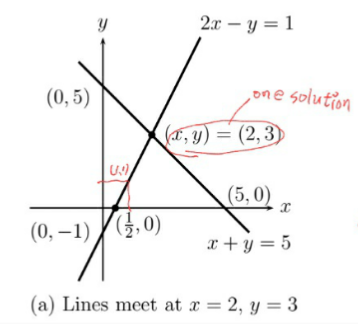
두 선의 교차점은 두 방정식의 해(solution)이 됩니다.
x = 2, y = 3은 소거법으로 찾을 수 있습니다.
2. 열(column) 접근

두 개의 방정식은 하나의 벡터(vector)방정식 입니다.

오른쪽 벡터를 만드는 왼쪽 열 벡터들의 결합을 찾을 수 있습니다.
이 벡터들(2,1)과 (-1,1)은 아래 그림처럼 굵은 직선들로 나타낼 수 있습니다.

미지수 x와 y는 열 벡터(column vectors)과 곱해집니다.
1번 열에 2곱하고, 2번 열에 3곱하면 오른쪽 항(1,5)가 됩니다.
기하학적으로 이것은 평행사변형을 만듭니다.
위 column picture에서 x=2, y=3을 확인할 수 있습니다.
다음 포스팅에서는 n=3인 경우에 row picture과 column picture를 알아보겠습니다.
반응형