이번 포스팅에서 공부할 것은 다음과 같습니다.
선형 방정식 - linear equation
선형 방정식 계 - sysyems of linea equation
해의 집합 - solution set
consistent/inconsistent 의미 - no solution, exactly one solution, infinity many solutions
행렬 표기법 - matrix notation
소거법 - elimination
행 연산 - row operation (replacement, interchange, scaling)
상등(equivalent)/ 행 상등(row equivalent)
1. 선형 방정식 - linear equation
$x_1, ... , x_n$ 변수로 이루어진 선형 방저식은 다음과 같이 쓸 수 있습니다.

여기서 b와 $a_1, ... , a_n$은 실수(real number) 혹은 허수(complex number)인 상수(coefficient)입니다.
선형 방정식이 아닌 경우를 살펴보겠습니다.

이 두 식은 선형 방정식이 아닙니다.
$x_1x_2$와 $\sqrt{x_1}$ 때문입니다.
2. 선형 방정식 계 - A system of linear equation
선형 방정식 계(a system of linear equation)은 선형 시스템(linear system)이라는 용어를 사용하기도 합니다.
선형 방정식 계는 같은 변수들을 포함한 선형 방정식이 1개 또는 그 이상의 집합을 의미합니다.
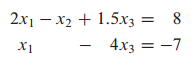
위 두 개의 선형방정식은 선형 방정식 계라고 할 수 있습니다.
3. 해의 집합 - Solution set
Solution set은 선형 시스템에서 모든 가능한 해의 집합을 의미합니다.
4. 상등 - equivalent
두 선형 시스템이 같은 solution set을 갖고 있다면 두 선형 시스템은 상등(equivalent)하다고 합니다.
즉, 같은 solution set을 갖은 선형방정식간의 관계를 행 상등(equivalent)라고 합니다.
5. 해가 있다(consistent), 해가 없다(inconsistent)
(1) 해가 없다. - inconsistent
inconsistent는 no solution을 의미합니다.
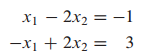
이 처럼 두 직선이 평행하게 되면 교차점이 없습니다.
이 경우에 no solution(해가 없다)이며, 두 방정식은 inconsistent 합니다.
(2) 해가 있다. - consistent
두 방정식이 consistent 관계에 있으면 (i) 해가 무수히 많다. (ii) 하나의 해가 있다. 두 가지 경우로 해석할 수 있습니다.
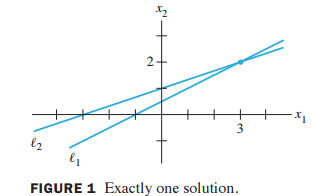
해가 하나인 경우
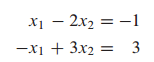
해가 무수히 많은 경우
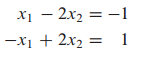

즉, 선형 방정식 계는 1. no solution, 2. exactly one solution, 3. infinitely many solution 세 가지 경우를 갖고 있습니다.
inconsistent는 1. no solution 을 의미하고
consistent는 2. exactly one solution, 3. infinitely many solution을 의미합니다.
6. 행렬 표기법 - matrix notation
행렬 표기법은 선형 시스템을 행렬로 표현한 것입니다.
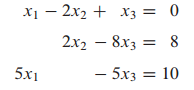
이 3개의 방정식을 행렬로 표기하면 다음과 같습니다.
(1) 계수 행렬 - coefficient matrix (3x3)
계수 행렬은 b를 제외하고 a만을 행렬로 나타낸 것입니다.
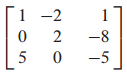
(2) 첨가 행렬 - augmented matrix (3x4)
첨가 행렬은 b까지 포함한 행렬입니다.

7. 소거법 - elimination
행 연산(row operation)을 통해 소거법(elimination)을 진행하고 선형 방정식(linear equation)의 해(solution)를 구할 수 있습니다.
linear algebra and its applications 책에 나와있는 소거법 절차입니다.

마지막 행의 $x_1$의 계수를 0으로 만듭니다.

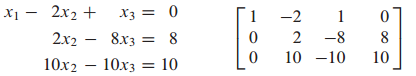
마지막 행의 $x_2$의 계수를 0으로 만듭니다.
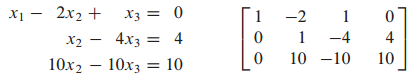
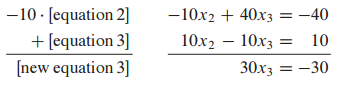
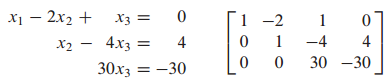
마지막 행의 $x_3$의 계수를 1로 만듭니다.

$x_3$을 알았으므로 대입을 이용해 $x_1, x_2$를 구할 수 있습니다.
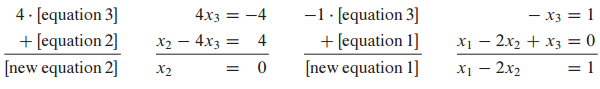
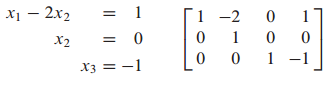

$x_1=1, x_2=0, x_3=-1$로 one solution을 갖고 있으므로 세 방정식은 consistent 합니다.
또한 같은 solution set을 갖고 있으므로 row equivalent 합니다.
8. 행 연산 - row operation
소거법(elimination) 절차에서 3가지 행 연산이 이용되었습니다.
(1) replacement
상수로 곱셈이 된 다른 행을 하나의 행에 더하는 행위
(2) interchange
두 개의 행을 바꾸기
(3) scaling
0이 아닌 상수로 행의 모든 항목을 곱하기
9. 행 상등 - row equivalent
행 연산 과정이 하나의 행렬을 다른 행렬로 변환된다면 두 행렬은 행상등(row equivalent) 하다고 할 수 있습니다.
두 선형 시스템이 행상등하다면 두 시스템은 동일한 해의 집합을 갖고 있습니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 1.3 벡터 방정식 - Vector Equations - Span{}, 선형 결합, 벡터의 대수학적 성질 (1) | 2020.10.26 |
|---|---|
| [선형대수학] 1.2 행 줄임과 사다리꼴 - Row reduction and Echelon forms - 기약 사다리꼴, 선행 성분, 자유 변수, 일반 해, 유일성 (0) | 2020.10.26 |
| [선형대수학] ch1-2 선형방정식의 기하학 - 특이한 경우 (0) | 2020.10.24 |
| [선형대수학] ch1.2 선형방정식의 기하학 - n=3인 경우 row picture과 column picture, 선형 결합 (0) | 2020.10.24 |
| [선형대수학] ch1.2 선형방정식의 기하학 - n=2일 때 행관점과 열관점 (0) | 2020.10.24 |