gilbert strang 교수님의 linear algebra and its applications를 공부하면서 번역과 정리를 해보았습니다.
Ch 1 행렬과 가우시안 소거법
1.1 개요 - Introduction
선형 방정식을 풀 때, 미지수와 방정식의 수가 같으면 가장 간단하고 쉽습니다.
미지수가 2개 방정식이 2개 인 경우를 보겠습니다.

미지수는 x와 y입니다.
위 선형방정식을 풀기 위해 소거법과 행렬식 두 가지 방법을 소개하겠습니다.
1. Elimination - 소거법

방정식2 - 4 X 방정식1을 하면 방정식2에서 x가 소거됩니다.
그러면 방정식2는 y에 대한 방정식이됩니다.
이것을 방정식1에 대입하면 x를 구할 수 있습니다.
2. Determinants - 행렬식
행렬식을 이용하면 위 선형방정식을 아래와 같이 적을 수 있습니다.
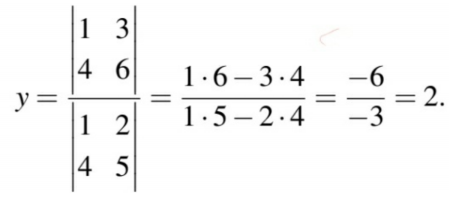
이것을 ratio of determinants라고 합니다.
이런식으로 x에 대한 행렬식도 적을 수 있습니다.

행렬식 방법은 1000개의 방정식에 대해서는 최악입니다.
n이 매우 큰 방정식을 풀기 위해서는 4장에서 배우는 cramer's rule이 효과적이긴 하지만 1장에서는 Gaussian Elimination(가우스 소거법)이 제일 좋은 방법입니다.
1장의 4가지 핵심
1. 선형방정식은 평면들의 기하학으로 나타냅니다.

10 차원 공간에서 9차원 평면을 시각화하기는 어렵지만 가능합니다.
위 예제에서 두 가지 직선을 기하학적으로 표현한 것입니다.
2. 행렬 표기법으로 나타낼 수 있습니다.
Ax = b에서 A를 LU로 분해하여 나타낼 수 있습니다.

L은 lower triangular, U는 upper triangular를 의미합니다.
모든 행렬은 transpose(전치) $A^T$를 갖고 있으며, 위에서 A 행렬은 inverse(역) $A^{-1}$를 갖고 있습니다.
3. 많은 경우에 어려움없이 소거법을 진행할 수 있습니다.
inverse(역)과 Ax=b system을 갖고 있는 행렬은 하나의 해를 갖고 있습니다.
하지만 특이한 경우에 소거법을 할 수 없습니다.
특이한 경우(singular case)에 대해 알아보겠습니다.
(1) 방정식이 잘못된 순서로 쓰여졌을 경우
이 경우에 순서를 바꿔서 풀 수 있습니다.
(2) the singular case(특이한 경우)
특이한 경우에는 해가 없거나 무수히 많은 해가 있습니다.

4. 시스템을 해결하기 위해 필요한 elimiation steps의 수를 대략적으로 계산해야 합니다.
컴퓨터는 많은 수의 방정식을 빠르게 처리할 수 있지만 1조개가 넘는 경우 수많은 단계를 거친 후에 반올림 에러(roundoff error)가 발생할 수 있습니다.