저번 포스팅에서 모든 matrix transformation은 linear transformation이므로
T(u+v) = T(u) + T(v)와 cT(u) = T(cu) 두 가지 linear 성질을 만족한다는 것을 배웠습니다.
이번 포스팅에서 공부할 내용은 다음과 같습니다.
행렬 변환 - matrix transformation
표준 행렬 - standad matrix
선형 변환 - linear transformation
onto
one-to-one
1. 행렬 변환 결정 방법 - How to determine a matrix transformation
Ax = T(x)에서 A를 모를 때 A가 어떤 요소로 이루어져있는지 알아보는 방법에 대해 공부하겠습니다.

I는 항등 행렬(Identity matrix)를 의미하고
$e_1,e_2$는 I의 column을 의미합니다.
T(x) = Ax를 의미합니다.
$R^2$ 정의역(domain)에서 $R^3$ 공역(codomain) 으로 변환해주는 A를 모르고
T(e)(e의 image)를 안다고 가정하겠습니다.
이 경우에 A가 무엇인지 찾을 수 있습니다.


항등 함수의 성질과 linear transformation의 특성을 이용하면 다음과 같이 표시할 수 있습니다.


즉 이것을 통해 A는 T(e)로 이루어져 있다는 것을 알 수 있습니다.
2. 이론(Theorem) 10
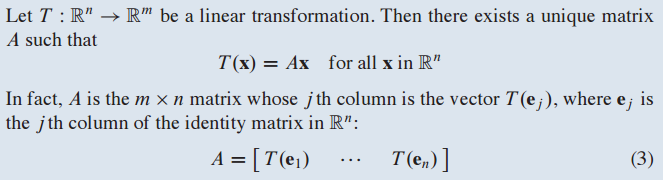
T(e)로 구성된 A를 standard matrix(표준 행렬) for the linear transformation T 라고 부릅니다.
$R_n$ space에 있는 identity matrix의 각각의 column을 transformation을 취한 결과 image를 column으로 갖고 있는 matrix를 표준 행렬(standard matrix)라고 합니다.
증명
vector x를 $I_n$x라고 표현해보겠습니다. I는 identity matrix 입니다.
아래 식은 x를 linear combination 형태로 표현한 것입니다.

linear 성질에 의해 T(x)는 다음과 같이 표현할 수 있습니다.


A는 T(e)의 열들로 구성되어 있으므로 표준 행렬(standard matrix)입니다.
3. 표준 행렬 예시 - Standard matrix Example

T는 $R^2$ domain에서 $R^2$ codomain으로 변환하는 함수입니다.

위 그림처럼 반시계 방향으로 회전하는 transformation을 찾아보겠습니다.
Identity matrix는 transformation 결과만 알면 transformation matrix를 알 수 있습니다.


A는 T(e)로 이루어져 있으므로 아래 식을 도출할 수 있습니다.

4. 2차원 실수 체계에서 기하학적인 선형 변환 - Geometric Linear Transformation of $R^2$
아래 표를 보면 Standard Matrix가 작동하는 방법을 시각적으로 이해할 수 있습니다.






5. Onto - Surjective, 전사 함수
Transformation에서 중요한 단어 onto와 one to one 2가지를 알아보겠습니다.
첫 번째는 Onto 입니다.
Onto는 임의의 y에 대해서 여러 개의 x가 존재한다는 것입니다.

이것을 Transformation에 적용해보겠습니다.


Dose T map $R^n$ onto $R^m$? 의미는 Does T(x) = b have at least one solution for each b in $R^m$을 의미합니다.
T의 range(모든 image set)가 모두 codomatin $R^m$에 있을 때 T는 $R^m$에 onto 합니다.
즉, codomain $R^m$에 있는 각각의 b에 대해 T(x)=b의 적어도 하나의 solution이 존재한다면 onto라고 할 수 있습니다.

$R^m$에서 T(x)가 T의 range에 포함되지 않는 경우가 있으면 not onto 입니다.
모든 $R^n$ space가 range 자체면 onto입니다.
임의의 b에 대해 최소 1개의 solution이 있으면 onto입니다.
6. One-to-one - injection, 단사 함수
정의역(domain)과 공역(codomain)이 원소 하나에 대응되는 것을 의미합니다.
일대일 함수와는 살짝 다른 점은 Y원소 개수와 X원소 개수가 같을 필요가 없습니다.
하지만 X원소 개수 <= Y원소 개수는 만족해야 합니다.


Is T one-to-one? 의미는 Does T(x) = b have either a unique solution or none at all?(해가 없거나 1개)을 의미합니다.

1:1 매칭이면 T is one-to-one
하나의 image가 여러 개의 vector에 해당된다면 T is not one-to-one 입니다.
7. onto와 one-to-one 예시 문제
Does the following T map $R^4$ onto $R^3$?
Is T a one-to-one mapping?

row 3개, pivot position이 3개 있으므로 solution이 존재합니다.
무조건 solution이 있으므로 $R^4$에서 $R^3$으로 onto합니다.
변수가 4개 pivot position이 3개 이므로 1개는 free variable입니다.
$x_3$이 free variable이므로 unique solution이 아니라 infinitely many solutions이므로 non one-to-one 입니다.
8. 이론(Theorem) 11

one-to-one은 solution이 최대 1개 or 0개를 의미합니다.
이론 11은 T가 one-to-one이면 T(x)=0 방정식은 자명해(x=0, trivial solution)만 갖는다는 이론입니다.
증명
T is one to one의 경우
trivial solution만을 갖게 됩니다.
따라서 T(0) = T(00) = 0T(0) = 0을 성립합니다.
만약 T is not one-to-one의 경우
T(u)=b, T(v)=b
one-to-one이 아니므로 b(image)는 여러 개의 vector와 매칭됩니다.(해가 여러개)
T(u-v) = T(u) - T(v) = 0에서 one-to-one이 아니므로 nontrivial solution을 갖게 되어
u - v != 0 을 성립합니다.
따라서 T(x)=0은 1개 이상의 solution을 갖고 있습니다.
9. 이론(Threorem) 12

T: $R^n$ -> $R^m$이 linear transformation이면 A는 T에 대한 standard matrix입니다.
T가 $R^n$ onto $R^m$이면 columns of A는 Span $R^m$입니다.
다르게 말하면, columns of A가 Span $R^m$이면 T는 $R^n$ onto $R^m$입니다.
T가 one-to-one이면 columns of A는 linearly independent입니다.
linearly independent는 trivial solution만을 갖는다는 의미입니다.
10. onto, one-to-one 판단 예시 문제

T map $R^2$ onto $R^3$과 T is a one-to-one mapping을 판단하는지 알아보겠습니다.
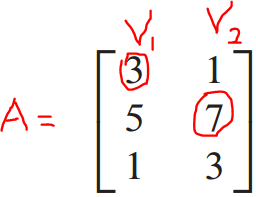
v1과 v2가 scalar multiplication으로 표현되지 않습니다.
이는 linearly independent를 의미합니다.
linearly independent는 trivial solution만 존재한다는 의미이므로 one-to-one이 성립합니다.
행렬 A는 3개의 행에 2개의 pivot position이 존재합니다.
모든 row가 pivot position을 갖고 있지 않으면 not onto 입니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
