이번에 공부할 내용은 행렬 연산(Matrix Operations)입니다.
행렬 표기법 - Matrix Notation
행렬 덧셈 - Matrix Sum
스칼라 곱 - Scalar Multiple
행렬 곱 - Matrix Multiplication
행렬의 전치 - The transpose of a matrix
1. 행렬 표기법 - Matrix Notation
A가 mxn 행렬이면 i번째 행, j번째 열에 있는 스칼라 항목은 $a_{ij}$로 표기합니다.
또한 A의 (i,j) 항목이라고 부릅니다.

2. 행렬 덧셈 - Matrix Sum
같은 사이즈 행렬 A와 B가 있으면 행렬 덧셈을 할 수 있습니다.
각각 모든 entry를 더하면 됩니다.

3. 스칼라 곱 - Scalar Multiple
r 스칼라와 A 행렬이 있으면 스칼라 곱(scalar multiple) rA를 할 수 있습니다.

4. 이론 1 - Theorem 1

Matrix A, B, C 가 있고 Scalar r, s가 있을 때 위 성질을 만족합니다.
이는 1장에서 공부했었던 $R^n$ 공간에서 vector의 성질과 동일합니다.
각각의 matrix는 column vector로 이루어져 있습니다.
따라서 vector의 성질을 만족하게 되어 위 성질을 만족하게 됩니다.
5. 행렬 곱 - Matrix Multiplication

행렬 곱(Matrix Multiplication)은 스칼라 곱(Scalar Multiplication)과 다릅니다.
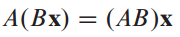
Matrix Multiplication은 matrix size가 중요합니다.
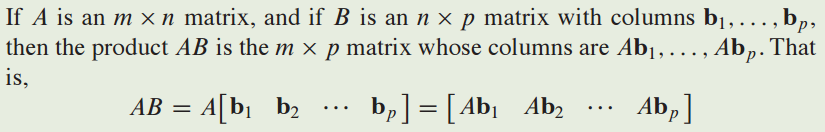
m X n matirx A와 n X p matrix B를 곱하면 m X p matrix AB를 생성합니다.
AB는 Ab1, Ab2, Ab3을 나열한 행렬입니다.
이전 chapter까지는 b1 하나의 vector에 대해 공부했는데 이번에는 b matrix가 b1~bp로 이루어진 matrix에 대한 내용입니다.


6. 이론 2 - Theorem 2

A, B, C가 같은 size를 갖고 있으면 위 성질을 만족합니다.
주의할 점은 AB는 BA와 다릅니다.

일반적인 실수 체계에서는 AB=BA가 성립하지면 matrix 체계에서는 성립하지 않습니다.

7. 행렬의 전치 - The Transpose of a Matrix

행렬의 전치(transpose of a matrix)는 column과 row를 바꾼 것입니다.

8. 이론 3 - Theorem 3
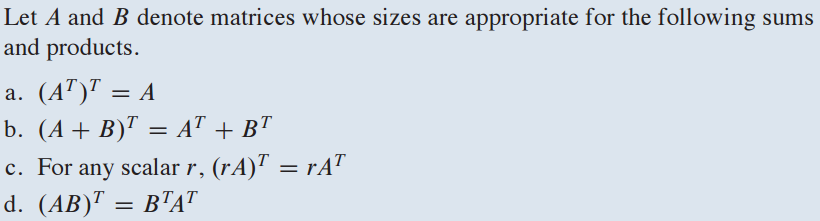
주의할 점은 성질 d 입니다.
전치를 하면 matrix의 size가 변하게 됩니다.
matrix multiplication은 matrix size가 같아야 하는 성질이 있으므로 순서를 바꿔 size를 동일하게 합니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
