반응형
이번 포스팅에서는 역행렬이 존재하는 행렬의 특징에 대해 알아보겠습니다.
1. 이론 8. 역행렬 이론 - Theorem 8. The Invertible Matrix Theorem

A가 invertible이면 위 조건을 다 만족하고 not invertible이면 위 조건을 만족하지 않습니다.
Ax = 0은 trivialsolution만을 갖으므로 independent, n pivot position을 만족합니다.
n개의 pivot position을 만족하므로 one-to-one도 성립하며
A는 solution이 있으므로 A는 R공간에 span하고, onto도 성립하게 됩니다.
2. 역선형 변환 - Invertible Linear Transformation

linear Transformation이 invertible이라고 불릴 조건은 다음과 같습니다.

x의 image에 S 함수를 위하면 원래 x로 돌아옵니다.
이처럼 S 함수가 존재하는 경우에 T는 invertible하다고 합니다.
3. 이론 9 - Theorem 9
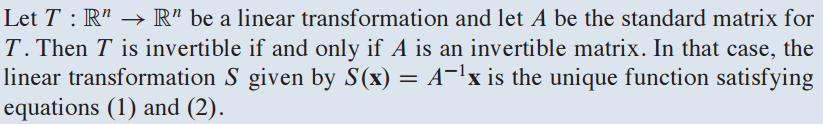
선형 변환(linear transformation)은 항상 표준 행렬(standard matrix)이 존재합니다.
T가 invertible이면 A(standard matrix)도 invertible 합니다.
또, 선형 변환(linear transformation) S 함수는 S(x) = $A^{-1}x$로 주어집니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

반응형