이번 포스팅에서는 LU 분해(LU deposition)에 대해 알아보겠습니다.
LU분해는 실제 문제를 해결할때 유용하게 쓰이므로 공대생에게 매우 중요합니다.
1. 분해 - Factorization, decomposition
분해는 하나의 행렬을 두개 혹은 3개 이상의 행렬 곱으로 표현한 식을 의미합니다.
A=BC
A 행렬을 B와 C의 곱으로 표현했는데 이런 형태를 분해(factorization)이라고 합니다.
2. LU 분해 - LU decomposition
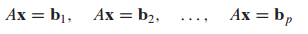
방정식을 푸는 방식은 크게 두 가지가 있습니다.
(1) A의 역행렬을 이용
이 경우에 $A^{-1}b_1, A^{-1}b_2$ 모든 경우를 구해야 하므로 비효율적입니다.
(2) LU 분해
행 줄임(row reduction)으로 A를 LU분해하여 방적식을 푸는 것이 효과적입니다.

L은 a unit lower triangular matrix를 의미하고
U는 echelon form을 의미합니다.
주의할 점은 U는 reduced echelon form이 아닙니다.
A를 분해해서 U로 변환할 때 row interchange, scaling 없이 replacement만을 이용해서 변환해야 합니다.
L은 diagonal term이 모두 1이고 아래는 nonzero entry인 행렬입니다.
nonzero entry에 zero가 들어가도 상관 없습니다.
diagonal term이 모두 1이어야만 하는 이유는 대각선이 1이 아니면 너무 다양하기 때문입니다.
3. LU 분해의 유용성

A=LU로 분해하였을 때 Ax=b 방정식을 다음과 같이 표현할 수 있습니다.
A=LU
Ax=b
위 방정식을 풀어보겠습니다.
LUx=b
Ux=y로 치환하여 대입합니다.
Ly=b y를 풉니다.
Ux=y U와 y를 알고있으므로 x를 풀 수 있습니다.
L과 U는 pivot을 사용해서 나머지 entry를 0으로 만들 수 있는 쉬운 형태로 이루어져 있기 때문에 빠르게 문제를 풀 수 있습니다.
4. LU 분해 예시 문제
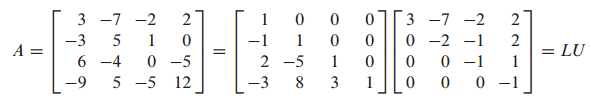

위 처럼 A와 b가 주어졌을 때 우선 Ly=b로 y를 구합니다.

Ux=y에서 U와 y를 알고 있으므로 x를 구할 수 있습니다.
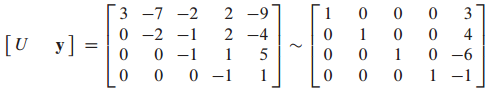
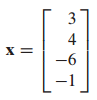
이처럼 L과 U를 알고 있으면 해를 구하기가 쉽습니다.
5. LU 구하는 방법 - LU decomposition Algorithm
A가 row replacement만을 사용해서 사다리 꼴(echelon form) 형태로 변환될 수 있다고 가정하겠습니다.
그렇게 되면 U(echelon form)로 변환하기 위한 행 줄임(row operation) 기본 행렬(elementary matrix) $E_1, ... ,E_p$가 존재합니다.
이 기본 행렬의 역행렬(inverse)이 L이 됩니다.
A가 m x n 행렬일 때 L과 U의 크기는 m x m, m x n이 되어야합니다.
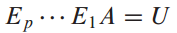
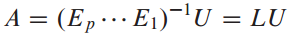


예시 문제를 살펴보겠습니다.
A가 다음과 같이 주어졌을 때 LU 분해를 해보겠습니다.

A가 4개의 행을 갖고 있으므로 L은 4 x 4가 되어야 합니다.
L을 구하기 위해 우선 U(echelon form)를 구해보겠습니다.
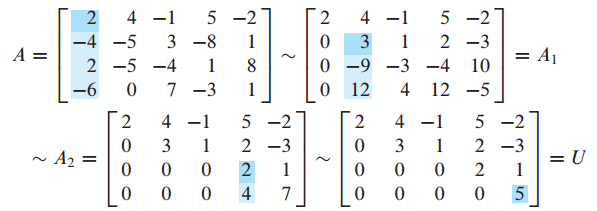
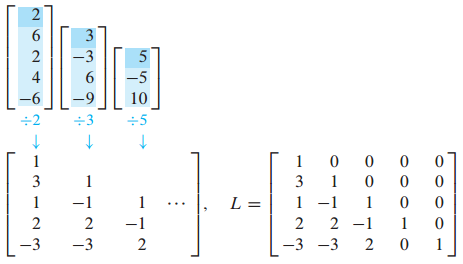
L은 A의 각각 pivot column에서 pivot 아래의 entry를 pivot으로 나눠주면 구할 수 있습니다.
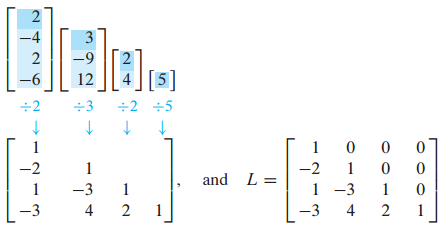
이해를 돕기 위해 다른 예시 문제도 살펴보겠습니다.

행 줄임(row reduction) 연산으로 U를 구합니다.

U를 구하는 과정에서 구한 A의 pivot column을 이용해서 L을 구합니다.
6. 수와 관련된 메모 - Numerical Notes

$A^{-1}$로 해를 구했을 때 보다 LU 분해의 연산량이 1/3배 적습니다.
또한 A가 sparse(대부분이 0으로 채워져있는 경우)하면 L과 U도 sparse합니다.
하지만 $A^{-1}$는 dense(값이 많은 경우)합니다.
이 의미는 L과 U를 저장하는 memory와 $A^{-1}$ 값을 저장하는 memory의 차이가 큰 것을 의미합니다.
공학적인 문제를 풀 때 LU 분해는 속도와 메모리적 측면에서 큰 이점을 얻을 수 있습니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
