[선형대수학] 3.1 행렬식 개요 - Introduction to Determinants - 행렬식, 여인수, 여인수 전개

이번 포스팅에서 알아볼 내용은

 

 행렬식 - determinant

 여인수 - cofactor

 여인수 전개 - cofactor expansion

 

입니다.

 

1. 2 x 2 Matirx

 2장에서 배운 것을 복습하면 2 x 2 행렬에서의 determinant가 nonzero이면 invertible입니다.

 

2. 3 x 3 역행렬이 존재하는 행렬 - 3 x 3 invertible matrix

 2 x 2 행렬의 determinant를 구하는 건 비교적 쉽습니다.

 3 x 3 이상 행렬 부터는 determinant를 구하는 것이 복잡해집니다.

 

 determinant가 0이 아닌 것의 의미는 모든 row에 pivot이 존재한다는 의미입니다.

 따라서 row reduction을 진행하고 모든 pivot이 nonzero임을 확인하면 됩니다.

 

 여기서 $\triangle$은 다음과 같습니다.

 A가 invertible이므로 $\triangle$은 nonzero이어야만 합니다.

 

 2 x 2 matrix에서 determinante는 아래와 같으므로 $\triangle$을 다음과 같이 표기할 수 있습니다.

 

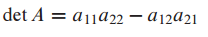
 $A_{13}$은 1th row와 3th column을 제외한 요소들을 의미합니다.

 A가 위와 같이 주어졌을 때 $A_{32}$은 다음과 같이 표기할 수 있습니다.

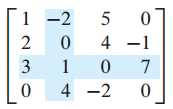
 3th row와 2th column을 제거하면 아래와 같이 됩니다.

 

3. 행렬식 - Determinant

 2 x 2 이상 matrix 일때 determinant 결정 방법은 다음과 같습니다.

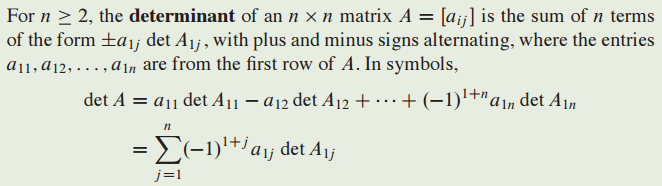
 determinant의 정의는 다음과 같습니다.

 

 예시 문제를 한번 살펴보겠습니다.

 A 행렬이 주어졌을 때 determinant를 계산하는 문제입니다.

 

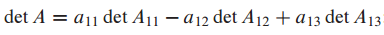
 determinant를 간단히 표현하면 아래와 같이 표현할 수 있습니다.

 

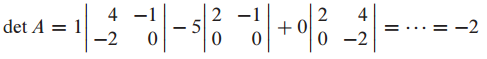
4. 여인수 - Cofactor

 cofactor를 이용해서 determinant를 여러가지 형태로 표현할 수 있습니다.

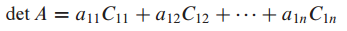
 이를 여인수 전개(cofactor expansion)라고 합니다.

 

 cofactor의 부호는 $(-1)^{i+j}$는 다음과 같은 규칙을 갖습니다. 

 

5. 이론 1 - Theorem 1

 cofactor expansion을 이용하면 임의의 row와 column으로 determinant를 표현할 수 있습니다.

 어떤 cofactor를 이용하더라도 결과는 동일합니다.

 cofactor를 이용할 때 zero가 많은 row나 column을 기준으로 cofactor expansion을 이용하면 계산이 단순해집니다.

 

 예시문제를 살펴보겠습니다.

 A가 주어졌을 때 det A를 cofactor expansion을 사용해서 계산하는 문제입니다.

 

예시문제 2

 0이 많이 구성되어 있는 matrix는 다음과 같이 cofactor expansion을 사용할 수 있습니다.

 first column에 0이 제일 많으므로 이를 기준으로 cofactor expansion을 사용합니다.

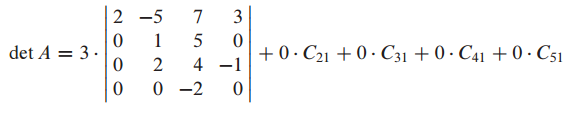
 first column에 0이 제일 많으므로 이를 이용합니다.

 이처럼 0이 많은 row나 column을 이용하면 cofactor expansion을 유용하게 이용할 수 있습니다.

 

6. 이론 2 - Theorem 2

 A가 삼각 행렬(triangular matrix)이면 det A는 A의 digonal term을 곱한 것입니다.

 

7. det EA = (det E)(det A)

 E는 기본 행렬(elementary matirx)를 의미합니다.

 det EA 는 (det E)(det A)와 동일합니다.

 $E_1$은 interchange, $E_2$는 second row k scaling

 $E_3$은 second row에 k scaling한 것을 first row에 더한 replacement

 $E_4$는 first row에 k scaling 한 것을 second row에 더한 replacement를 의미합니다.

 

 각각의 det은 다음과 같습니다.

 

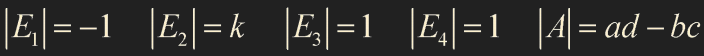
 det EA = (det E)(det A)를 증명하는 과정입니다.

 

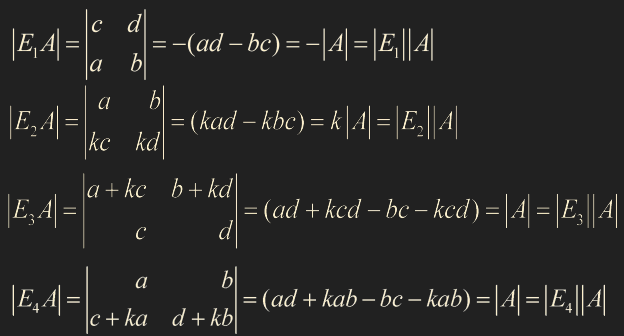
8. 수치적인 메모 - Numerical Note

 이는 cofactor expansion이 복잡하다는 내용입니다.

 cofactor expansion으로 det를 구하는 연산은 n!이 소요되므로

 det를 cofactor expansion으로 계산하는 것은 멍청한 짓이라는 말로 해석할 수 있습니다.

---

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.