이번 포스팅에서 배울 내용은
행 연산에 의한 행렬식 변화 - Determinant changes by row operations
det $\neq$ 0
det $A^T$ = det A
det AB = (det A)(det B)
입니다.
1. 이론 3. 행 연산 - Theorem 3. Row Operations

a. A의 하나의 row 곱이 다른 row에 더해져 B 행렬이 만들어지면 det B = det A 입니다.
이는 row replacement를 의미합니다.
b. B를 만드기 위해 A의 두개의 row가 interchange 됬으면 det B = -det A 입니다.
c. A의 하나의 row에 k가 곱해져 B가 만들어졌으면 det B = k det A 입니다.
scaling을 의미합니다.
이 세가지 성질을 이용해서 row reduction을 통해 echlon form을 만든 후 cofactor expansion을 이용하면 det를 쉽게 구할 수 있습니다.
이전 포스팅에서 det EA = (det E)(det A)와 det E = 1, -1, r 이라는 것을 배웠습니다.
B는 A 행렬에 row reduction을 사용하여 만들어진 echelon form이라고 가정하면 B = EA로 표현할 수 있습니다.
각각의 row operation은 두 개의 row에 영향을 끼치므로 영향을 받지 않은 row를 기준으로 cofactor expansion을 사용하면 det A를 쉽게 구할 수 있습니다.
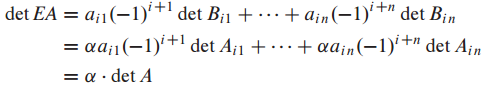
예시 문제

row reduction을 사용하여 echelon form으로 변환하면 det A를 쉽게 구할 수 있습니다.
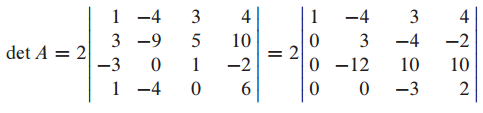

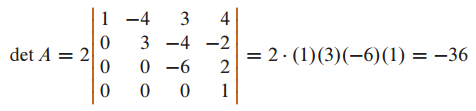
echelon form은 triangular matrix이므로 각각의 diagonal term을 곱하면 det을 구할 수 있습니다.
이는 echelon form에서 각각의 pivot들의 곱을 의미합니다.
또한 row operation 성질을 이용해서 elementary matrix의 det를 곱하면 det A가 나오게 됩니다.
이를 간단히 정리하면 다음과 같습니다.

A가 not invertible이면 pivot이 0인 row가 존재하게 되어 pivot들의 곱이 0이 되게 됩니다.
따라서 det A = 0이 됩니다.
2. 수치적인 메모 - Numerical notes

cofactor expansion을 사용해서 determinant를 구하면 n!의 연산이 필요합니다.
하지만 row operation을 이용하면 방법은 $2n^3/3$의 연산이 필요하므로 25 x 25이상의 행렬도 빠르게 계싼할 수 있습니다.
3. 이론 4. - Theorem 4

det A = 0이 아니면 A는 invertible 입니다.
A가 not invertible이면 det A = 0 입니다.
예를 들어 A가 다음과 같이 주어졌을 때 det A = 0이 나오므로 A는 not invertible matrix입니다.

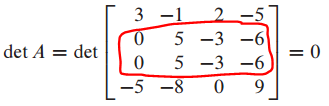
4. 이론 5 - Theorem 5

$A^T$의 det과 det A는 동일합니다.
5. 이론 6. 곱셈의 성질 - Multiplicative Property

det AB = (det A)(det B) 입니다.
A와 B가 다음과 같이 주어졌을 때 det AB = (det A)(det B)가 성립하는지 확인해보겠습니다.

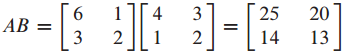
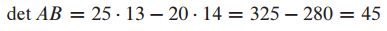

이를 통해 det AB = (det A)(det B)가 성립하는 것을 확인할 수 있습니다.

주의할 점은 det(A + B)는 det A + det B와 동일하지 않습니다.
6. 이론 6의 증명
이론 6은 det AB = (det A)(det B)가 동일하다는 이론입니다.
(1) A is not invertible
A가 not invertible이라면 det A = 0이고 det AB = 0 이므로 이론 6이 성립하게 됩니다.
(2) A is invertible
A는 invertible이므로 A를 항등 행렬(identity matrix)에 elementary matrix의 곱으로 표현할 수 있습니다.

따라서 det AB는 다음과 같이 표현할 수 있습니다.

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.
