이번 포스팅에서 특성 방정식(Characteristic equation)에 대해 알아보겠습니다.
characteristic equation은 eigenvalue와 밀접한 관련이 있는 equation입니다.
저번 포스팅에서 공부했던 것을 복습하자면
주어진 A 행렬의 eigen value를 구할 때 (A - $\lambda$I)x = 0 을 이용합니다.



A가 eigen value를 갖고 있으려면 Ax=0에서 nontrivial solution을 갖고 있어야 합니다.
이는 A가 not invertible을 의미하고 det(A) = 0이 되어야 합니다.



이를 통해 eigenvalue는 3,7 인것을 확인할 수 있습니다.
1. 특성 방정식 - The Characteristic Equation
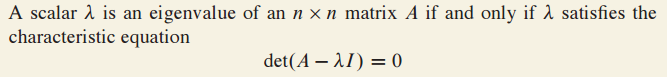
characteristic equation은 det(A-$\lambda$I) = 0을 의미합니다.
$\lambda$가 characteristic equation을 만족하면 $\lambda$는 행렬 A의 eigenvalue 입니다.
예시 문제
행렬 A의 characteristic equation을 찾는 문제입니다.
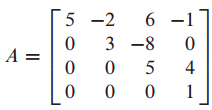
A는 upper triangular matrix입니다.
따라서 diagonal term이 eigenvalue가 됩니다.
det은 diagonal term의 곱 입니다.



eigenvalue는 5,3,1이 됩니다.
여기서 eigenvalue 5는 multiplicity 2를 갖습니다.
2. 유사도 - Similarity
n차 방정식에서 eigenvalue를 찾는 것은 쉽지 않아 similarity를 주로 이용합니다.
A = PB$P^{-1}$이 성립할 때 A는 B에 similar 이라고 표현합니다.
similarity transformation은 A = $P^{-1}$AP로 변환하는 transformation을 의미합니다.
3. 이론 3. - Theorem 3
eigenvalue를 찾는 방법으로 한가지를 소개하자면,
similar한 matrix를 찾아서 eigenvalue를 찾습니다.
일반적인 경우에 eigenvalue를 구하는 것은 다루기가 어려우므로 특수한 성질을 갖은 matrix의 eigenvalue는 상대적으로 쉽게 구할 수 있습니다.

A와 B가 similar이고 동일한 characteristic polynomial을 갖고 있으면 두 행렬은 동일한 eigenvalue를 갖습니다.
eigenvalue는 동일하지만 eigen vector space는 보통 다릅니다.
증명


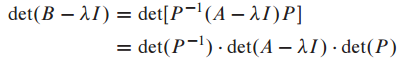
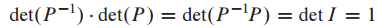

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 4.4 고유벡터와 선형변환(Eigenvectors and Linear Transformation) (0) | 2020.12.08 |
|---|---|
| [선형대수학] 4.3 대각화(Diagonalization), 행렬 대각화하기 (0) | 2020.12.07 |
| [선형대수학] 4.1 고유벡터와 고유값 - Eigenvectors and eigenvalue (0) | 2020.11.30 |
| [선형대수학] 3.3 크라메이 법칙, 부피 그리고 선형 변환 - Cramer's Rule, Volume and Linear Transformations (0) | 2020.11.22 |
| [선형대수학] 3.2 행렬식의 성질 - Properties of Determinants (0) | 2020.11.20 |