이번에 공부해볼 내용은 고유벡터와 선형변환의 관계입니다.
1. 선형 변환의 행렬 - The matrix of Linear Transformation

V가 n-dimensional vector space이고 W는 m-dimensional vector space로 주어졌을 때 V와 W를 연결시켜주는 T linear transformation을 가정하겠습니다..
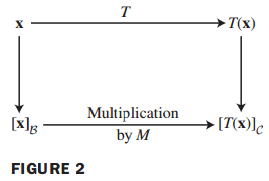
그러면 B basis로 표현되는 x의 coordinate vector $[x]_B$와 C basis로 표현되는 T(x)의 coordinate vector $[T(x)]_C$를 연결시키는 행렬이 있는지에 대한 궁금증이 생깁니다.
$[x]_B$와 $[T(x)]_C$ 사이의 연결은 쉽게 찾을 수 있습니다.
V에 대한 basis B가 {$b_1, ... ,b_n$} 로 구성되어 있다고 가정하겠습니다.
그러면 x는 다음과 같이 정의할 수 있습니다.

따라서 basis B에 대한 coordinate vector $[x]_B$는 다음과 같습니다.

그리고 T(x)는 다음과 같이 정의됩니다.

basis C에 대한 T(x)의 coorbinate vector는 다음과 같이 구할 수 있습니다.

이를 행렬 M을 이용해 간단히 표현하면 다음과 같습니다.
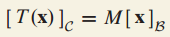
여기서 M은 다음과 같습니다.

행렬 M을 B와 C에 상대적인 T에 대한 행렬이라고 부릅니다.
예시 문제
vector space V, W에 대한 basis B, C와 T(b)가 주어졌을 때 basis B와 C에 상대적인 T에 대한 행렬 M을 찾는 문제입니다.

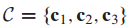

M = $[T(b)]_c$ 이므로 다음과 같이 구할 수 있습니다.
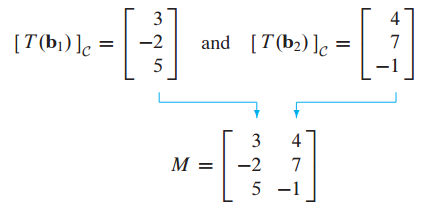
2. 동일한 벡터 공간에서 선형 변환 - Linear transformations from V into V
동일한 벡터 공간에서 선형 변환을 살펴보겠습니다.
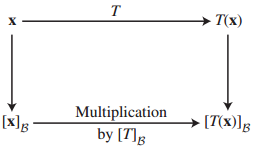
동일한 벡터 공간에서 선형 변환은 다음과 같이 정의됩니다.
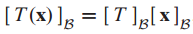
이를 B-matrix for T라고 간단히 표현합니다.
예시 문제
T가 $P_2 -> P_2$로 mapping한다고 정의되고 T(x)는 다음과 같습니다.
P는 polynomial space를 의미합니다.
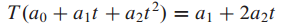
(1) B basis가 {1, t, $t^2$} 일 때 B-matrix for T를 찾고 (2) $[T(p)]_B]$ = $[T]_B[p]_B$를 증명하는 문제입니다.
(1)
T(b)는 다음과 같습니다.

T(b)를 구했으므로 $[T(b)]_B$는 다음과 같습니다.
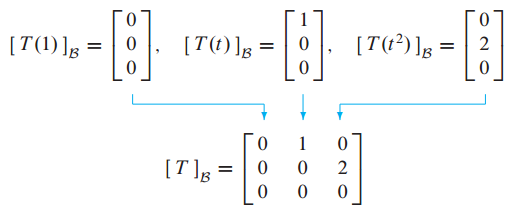
(2)
P(t) = $a_0 + a_1t + a_2t^2$ 에 대해서 $[T(p)]_B$는 다음과 같이 구할 수 있습니다.
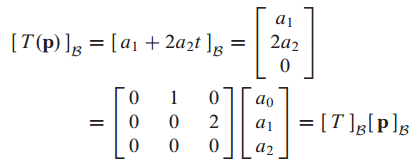
따라서 $[T(p)]_B]$ = $[T]_B[p]_B$ 는 증명되었습니다.

3. 이론 7. 대각 행렬 표현 - Theorem 7. Diagonal Matrix Representation

D는 diagonal matrix이고 A는 diagonalizable로 가정할 때 basis B는 P의 column으로 구성됩니다.
그리고 D는 b-matrix for T가 됩니다.
증명
P의 column은 $b_1, ... ,b_n$이므로 B = {$b_1, ... ,b_n$} 입니다.
따라서 P는 change-of-coordinates matrix $P_B$입니다.
그러므로 다음과 같은 성질을 만족합니다.

만약 T(x) = Ax이면 다음과 같습니다.

A = $PDP^{-1} 이므로 $[T]_B$는 다음과 같습니다.
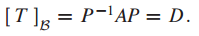
4. 행렬의 유사도 표현 - Similarity of Matrix Representations

A와 C가 similar이면 B-matrix는 C 입니다.
C가 꼭 diagonal matrix가 아니어도 성립합니다.

예시 문제

A와 basis가 주어지고 B-matrix를 찾는 문제입니다.
여기서 A의 eigenvalue는 -2 (multiplicity = 2)이고 eigenspace dimension =1 이므로 not diagonalizable 입니다.
$b_1, b_2$는 서로 곱의 관계가 아니므로 linearly independent 인것을 알 수 있습니다.
따라서 P를 구할 수 있습니다.

$A = PCP^{-1}$ 이므로 C는 다음과 같이 구할 수 있습니다.
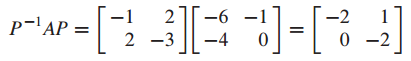
C의 diagonal entries가 A의 eigenvalue가 되고 B-matrix 입니다.
A가 diagonalizable이 아니더라도 어떤 independent basis만 선택한다면 B-matrix를 찾을 수 있습니다.
이때 basis는 independent set 이어야 합니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 5.2 직교 집합(Orthogonal Sets)과 정사영(Orthogonal Projection) (1) | 2020.12.23 |
|---|---|
| [선형대수학] 5.1 내적(Inner Product), 길이(Length) 그리고 직교성(Orthogonality) (0) | 2020.12.22 |
| [선형대수학] 4.3 대각화(Diagonalization), 행렬 대각화하기 (0) | 2020.12.07 |
| [선형대수학] 4.2 특성 방정식 - The Characteristic Equation - 유사도(similar), similar transformation (0) | 2020.12.05 |
| [선형대수학] 4.1 고유벡터와 고유값 - Eigenvectors and eigenvalue (0) | 2020.11.30 |