1. 직교 집합(Orthogonal Sets)
벡터의 집합 {$u_1, ... ,u_p$}이 존재할 때, 집합의 모든 벡터 쌍이 직교(orthogonal)이면 직교 집합이라고 합니다. 즉 $u_i\cdot u_j$ = 0 입니다.
직교 집합 {$u_1,u_2,u_3$}이 주어졌을 때, 각각의 벡터를 내적해보겠습니다.
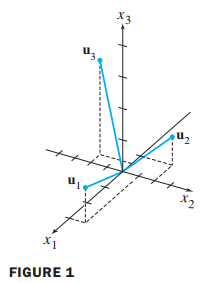

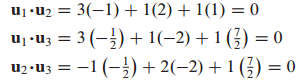
이처럼 각각의 벡터 쌍의 내적은 0이 됩니다.
2. 이론 4

S가 non-zero 벡터들의 직교 집합이면 S는 선형 독립(linearly independent)이고, 직교 집합은 S를 span하는 기저(basis)입니다.
증명
S의 직교 집합의 선형 결합(linear combination)이 0이라고 가정하겠습니다.
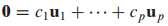
양변에 $u_1$을 곱하겠습니다.
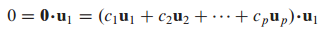
서로 다른 벡터의 내적은 직교이므로 0이 됩니다.

$u_1$은 non zero 이므로 $c_1$ = 0이 되어야 식이 성립하게 됩니다.
이것을 모든 벡터로 적용하면 $c_1, ... ,c_p$ = 0이 도출됩니다.
이는 자명해(trivial solution)이므로 S의 직교 집합은 선형 독립이 됩니다.
3. 직교 기저(Orthogonal basis)

부분 공간 W에 대한 직교 기저는 W에 대한 기저이고 직교 집합입니다.
각각의 기저가 서로 직교한다는 의미입니다.
책에서 직교 기저는 nice한 성질을 지니고 있다고 설명합니다.
4. 이론 5

W에 대한 직교 기저가 주어졌을 때, W에 존재하는 임의의 벡터 y를 직교 기저의 선형 결합으로 나타내면 가중치가 주어집니다.
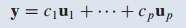
이전에는 가중치를 찾기 위해서 행 줄임(row reduction)을 통해 가중치의 해를 찾았는데, 직교 기저인 경우 가중치 공식이 주어집니다.
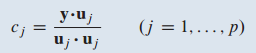
증명
위 선형 결합 식에서 양변에 $u_1$을 곱합니다.

$u_1, ... ,u_p$는 직교하므로 서로 내적하면 0이 나옵니다 따라서 $c_1(u_1\cdot u_1)$만 남게 됩니다.
이를 c에 대한 식으로 정리하면 다음과 같이 도출됩니다.

예시 문제
y와 직교 기저 $u_1, u_2, u_3$이 주어졌을 때 y를 선형 결합으로 표현하는 문제입니다.
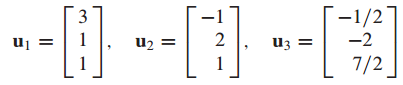



5. 정사영(Orthogonal Projection)
직교 기저 {$u_1, ... ,u_n$}이 주어지고, 직교 기저의 선형 결합으로 표현되는 벡터 y가 주어졌다고 가정하겠습니다.
이때, 벡터 y를 두 개의 직교 벡터의 선형 결합으로 분해하는 문제를 고려할 때, 다음과 같이 적을 수 있습니다.



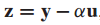
그림으로 표시하면 다음과 같습니다.

z와 $\hat{y}$는 직교하므로 내적은 0입니다.

이때, $\alpha$는 다음과 같이 구할 수 있습니다.

따라서 $\hat{y}$는 다음과 같이 됩니다.

이 $\hat{y}$를 u에 onto한 y의 정사영(orthogonal projection)이라고 하고, z를 u에 직교한 y의 요소라고 합니다.
그리고 다음과 정사영을 다음과 같이 표기합니다.

예시 문제 1
y와 u가 주어졌을 때, y를 u에 정사영하고, y를 두 개의 직교 벡터의 합으로 표현하는 문제입니다.

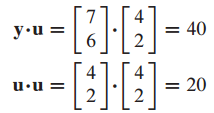


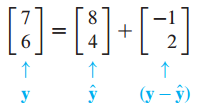
예시 문제 2

y와 직선 L의 거리를 구하는 문제입니다.
y, u는 예시문제 1에서 주어진 것과 동일합니다.
y에 y를 u에 정사영한 벡터를 빼면 가장 가까운 거리를 구할 수 있습니다.
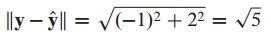
6. 정규직교집합(Orthonormal Sets)
집합 {$u_1, ... ,u_p$}가 유닛 벡터(unit vector)의 직교 집합이면 이는 정규직교집합입니다.
예시 문제
벡터 세개가 주어졌을때, 정규직교집합인지 판단하는 문제입니다.


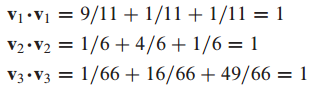
각 벡터의 길이가 1이고 각각의 벡터의 내적이 0이므로 정규직교집합입니다.
7. 이론 6

mxn 크기의 행렬 U가 정규직교 열들로 이루어져 있으면 $U^TU$ = I 입니다.
증명
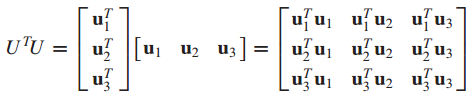
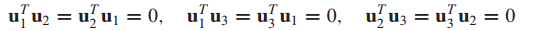

8. 이론 7

U가 정규직교 열로 이루어진 행렬이면 다음 3가지의 조건을 만족합니다.
예시 문제
U와 x가 주어졌을 때 Ux의 길이와 x의 길이가 같은지 확인하는 문제입니다.


이처럼 길이가 같은 것을 확인할 수 있습니다.
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 5.4 그람슈미트 과정과 QR 분해(Gram-Schmidt process and QR factorization) (1) | 2020.12.27 |
|---|---|
| [선형대수학] 5.3 정사영(Orthogonal Projections) (2) | 2020.12.27 |
| [선형대수학] 5.1 내적(Inner Product), 길이(Length) 그리고 직교성(Orthogonality) (0) | 2020.12.22 |
| [선형대수학] 4.4 고유벡터와 선형변환(Eigenvectors and Linear Transformation) (0) | 2020.12.08 |
| [선형대수학] 4.3 대각화(Diagonalization), 행렬 대각화하기 (0) | 2020.12.07 |