이번 포스팅에서는 그람슈미트 과정(Gram-Schmidt process)와 QR 분해(QR factorization)에 대해 공부해보겠습니다.
그람슈미트 과정은 임의의 부분공간(subspace)이 있을 때 그 subspace를 이루는 직교 기저(orthogonal basis)를 찾는 것입니다.
1. 그람슈미트 과정의 기본 아이디어(Basis idea for the Gram-Schmidt process)
2차원 공간
W = Span{$x_1, x_2$}라고 가정할 때, W에 대한 직교 기저(orthogonal basis) {$v_1, v_2$} 를 찾아보겠습니다.
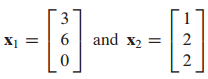
$v_1$ = $x_1$로 둡니다.
그리고 $v_2$는 $x_2$에서 $x_2$를 $x_1$에 projection 한 것을 빼주면 다음과 같이 표현 됩니다.

이 $v_2$는 $v_1$과 직교하게 되므로 W에 대한 직교 기저를 만든 것입니다.

3차원 공간
이번에는 2차원 평면 W가 아닌 3차원 공간 W가 주어졌다고 가정해보겠습니다.
$x_1,x_2,x_3$이 주어지고 이 벡터들은 선형 독립(linearly independent)하고 W를 span한다고 가정하겠습니다.

x를 이용해서 W에 대한 직교 기저 v를 구하는 법을 알아보겠습니다.
(1) $v_1$ = $x_1$로 둡니다.
(2) $v_2$는 $x_2$에 $x_2$를 $x_1$에 projection 한 것을 빼서 구할 수 있습니다.

$v_2$는 $x_1$에 직교한 $x_2$의 요소이므로 {$v_1, v_2$}는 W에 대한 직교 기저라고 할 수 있습니다.
(3) $v_3$을 $x_3$에서 $x_3$을 2차원 W에 projection 한 것을 빼서 구할 수 있습니다.
$x_3$을 2차원 W에 projection 한 것은 W를 span하는 각각의 orthogonal basis에 projection 한 뒤 그것들을 더해주면 됩니다.


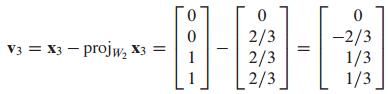
이제 $v_1, v_2, v_3$이 W를 span하는 orthogonal basis가 됩니다.
2. 이론 11 그람슈미트 과정(The Gram-Schmidt process)
위 과정을 정리한 이론입니다.

3. 정규직교 기저(Orthonormal basis)
정규직교 기저(orthonormal basis)는 직교 기저(orthogonal basis)로부터 손쉽게 구할 수 있습니다. 단순히 직교 기저들을 normalize 하면 됩니다.
normalize는 이전 포스팅에서 배웠던 벡터의 길이가 1이 되도록 하는 방법입니다.
예제 문제
orthogonal basis $v_1, v_2$가 주어졌을 때 orthonormal basis $u_1, u_2$를 구하는 문제입니다.
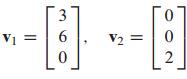
단순히 normalize 해주면 됩니다.

4. 행렬의 QR 분해(QR Factorization of Matrices)

column이 선형 독립(linearly independent)인 mxn 크기의 행렬 A는 A=QR로 분해될 수 있습니다.
여기서 Q는 column이 Col A에 대한 orthonormal basis로 이루어진 mxn 크기의 행렬이고
R은 nxn 크기의 모든 대각 요소가 양수를 가진 역행렬이 가능한(invertible) upper triangular 행렬입니다.
증명
A의 column이 Col A에 대한 기저 {$x_1, ... ,x_n$}로 구성되어 있습니다.
W = Col A에 대한 정규직교 기저 {$u_1, ... ,u_n$}를 구하기 위해서 그람슈미트 과정을 이용합니다.
그러면 Q를 구할 수 있습니다.

Col A의 basis x는 Col A의 orthonormal basis u의 선형 결합(linear combination)으로 표현할 수 있습니다.

이것은 $x_k$가 Q의 column들의 선형 결합으로 나타낼 수 있다는 의미입니다.
각각의 가중치(weight)들을 벡터로 표현하면 다음과 같습니다.
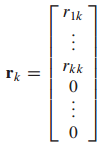
x는 Q와 가중치 r로 표현할 수 있으므로 다음과 같은 식이 성립합니다.
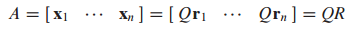
5. QR 분해 단계(QR Factorizaion Steps)
QR 분해 단계에 대해 알아보겠습니다.
(1) 그람슈미트 과정(Gram-Schmidt)으로 Col A에 대한 정규직교 기저(orthonormal basis)를 찾습니다.
이것이 Q가 됩니다.
(2) R은 다음과 같이 찾을 수 있습니다.

Q는 orthonormal basis의 column을 지니고 있으므로 $Q^TQ$는 Q의 길이를 의미합니다.
orthonormal basis의 길이는 1이므로 Q의 길이도 1이 됩니다. 따라서 항등행렬 I가 됩니다.
만약 R의 대각 요소 $r_{kk}$가 음수이면 $u_k$의 부호를 바꾸고 $r_{kk} ~ r_{kn}$ 부호를 바꿔줍니다.
예시 문제
행렬 A가 주어지고 A를 QR 분해하는 문제입니다.
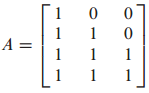
A의 각 column이 선형 독립(linearly independent)이어야지 QR 분해를 할 수 있습니다.
그람슈미트 과정으로 Q를 구합니다.


R을 구하는 공식으로 R을 구할 수 있습니다.

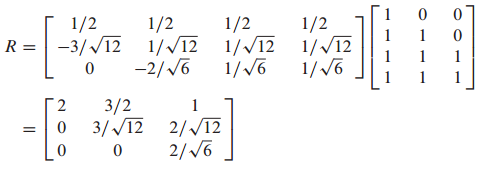
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
|---|---|
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |
| [선형대수학] 5.3 정사영(Orthogonal Projections) (2) | 2020.12.27 |
| [선형대수학] 5.2 직교 집합(Orthogonal Sets)과 정사영(Orthogonal Projection) (1) | 2020.12.23 |
| [선형대수학] 5.1 내적(Inner Product), 길이(Length) 그리고 직교성(Orthogonality) (0) | 2020.12.22 |