David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

대칭 행렬의 대각화는 선형대수학의 꽃인 SVD를 유도하기 위해 필요합니다.
대칭 행렬이 무엇이고 대칭 행렬을 대각화할때 나타나는 새로운 특성을 알아보도록 하겠습니다.
대칭 행렬(Symetric Matrix)
대칭 행렬은 행렬 A가 정사각 행렬(square matrix)이고, $A^T = A$를 만족하는 행렬입니다.
1) A가 정사각 행렬(square matrix)
2) $A^T = A$
위 두 가지 조건을 만족하면 대칭 행렬입니다.
대칭 행렬의 예시를 살펴보겠습니다.
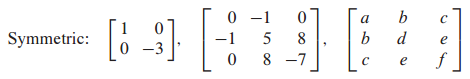
대칭 행렬이 아닌 경우입니다.

대각화(Diagonalization)
대칭 행렬의 대각화를 살펴보기 전에 이전에 배웠던 대각화를 복습해보겠습니다.
만약 A가 대각 행렬(diagonal matrix)와 유사(similar)하면 A를 대각화가능(diagonalizable)하다고 합니다.
즉, $A = PDP^-1$ 이면, A는 diagonalizable 입니다.
대각화 예시 문제
행렬 A가 다음과 같이 주어졌을 때, 대각화하는 문제입니다.

행렬 A는 대칭(symmetric) 행렬입니다.
대각화를 하기 위해 대각 행렬 D를 만들어야 합니다.
이는 특성 방정식(characteristic equation)으로 고유치(eigen value)와 고유 벡터(eigen vector)를 구해야 합니다.

위 식으로부터 고유치와 고유 벡터를 구할 수 있습니다.
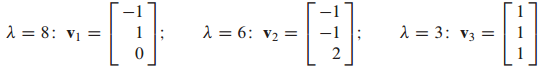
이 3개의 고유 벡터 {$v_1, v_2, v_3$}은 직교(orthogonal) 입니다.
각각의 벡터를 내적하여 쉽게 확인할 수 있습니다.
그리고 eigen vector이므로 선형 독립 집합(linear independent set)입니다.
이제 이 3개의 벡터를 정규화(normalize)하여 orthonormal vector로 표현하겠습니다.

P는 column이 eigenvector로 이루어진 행렬이고
D는 diagonal term이 eigenvalue로 이루어진 대각 행렬입니다.
따라서 P, D는 다음과 같이 표현할 수 있습니다.
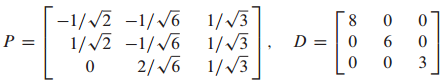
P의 column이 orthonormal vector로 이루어져 있으므로 $P^T = P^{-1}$ 입니다.
A 행렬을 대각화하면 $A=PDP^T$로 나타낼 수 있습니다.
위 문제를 풀면서 대칭 행렬의 eigenvector가 orthogonal 인것을 확인할 수 있었습니다.
이것은 우연이 아닙니다. 대칭 행렬의 특성입니다.
A 행렬이 대칭 행렬이면, 고유 벡터는 직교합니다. 이것을 이론화 한것이 이론 1 입니다.
왜 고유 벡터가 직교하는지 알아보도록 하겠습니다.
이론 1

A 행렬이 대칭이면 서로 다른 고유공간(eigenspace)에 있는 어떤 두 고유 벡터는 직교합니다.
증명
$v_1, v_2$가 서로 다른 고유치 $\lambda_1, \lambda_2$에 해당하는 고유 벡터일 때, $v_1\cdot v_2 = 0$임을 증명해보겠습니다.

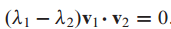
위와 같은 식이 나오게 되는데,

두 고유치는 서로 다른 값이므로 차는 0이 아닙니다.
따라서 고유 벡터 $v_1, v_2$의 내적이 0일 수 밖에 없습니다.

이러한 대칭 행렬의 성질 때문에 대칭 행렬의 대각화를 orthogonally diagonalizable 하다고 합니다.
아래에서 orthogonally diagonalizable에 대해 더 알아보겠습니다.
직교 대각화 가능(Orthogonally Diagonalizable)
만약 $A = PDP^T = PDP^{-1}$가 성립하면 행렬 A는 orthogonally diagonalizable 입니다.
여기서, P는 정규 직교(orthonormal) 벡터로 이루어진 직교 행렬(orthogonal maxtrix)이고, $P^{-1} = P^T$를 성립합니다. D는 대각 행렬입니다.
대칭 행렬이 orthogonally diagonalizable 하다는 것은 중요한 성질입니다.
대칭 행렬은 $A=A^T$를 만족합니다.
실제로 A가 orthogonally diagonalizable할 때, $A=A^T$를 만족하는지 확인해보겠습니다.
orthogonally diagonalizable이면 $A = PDP^T = PDP^{-1}$가 성립합니다.
양변을 전치하면 다음과 같은 결과가 나오게 됩니다.
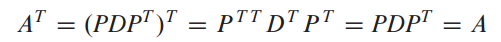
따라서 A는 대칭행렬입니다.
이론 2

이론 2번은 A 대칭행렬이 A가 orthogonally diagonalizable한다는 것과 동치를 의미합니다.
직교 대각화(orthogonally diagonalization) 예시 문제
주어진 행렬 A를 orthogonally diagonalization하는 문제입니다.
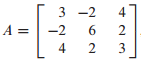
(1) 특성 방정식으로 고유치를 구합니다.
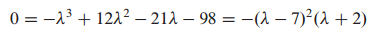
(2) 고유치에 해당하는 고유벡터를 구합니다.
고유치가 7일 때, multiplicity가 2입니다. A가 대각행렬일 때, 고유공간(eigenspace)의 dim은 multiplicity와 동일합니다.
따라서 두 고유벡터는 고유공간을 span하는 basis이므로 선형 독립입니다.

(3) 그람-슈미트 과정(Gram-Schmidt process)로 각 교유공간(eigenspace)에 해당하는 직교 기저(orthogonal basis)를 찾습니다.
고유치 7은 multiplicity가 2이므로 고유 벡터가 두 개 존재합니다. 이 둘은 선형 독립이지만 직교하진 않습니다. 그람-슈미트 과정(Gram-Schmidt process)로 두 고유 벡터를 직교하도록 만듭니다.

(4) 각각의 고유 벡터들을 정규화(normalization)하여 정규 직교 기저(orthonormal basis)를 얻습니다.


(5) 이 벡터들과 고유치로 P, D 행렬을 만듭니다.

이론 3 스펙트럼 정리(Spectral theorem)
행렬 A의 고유치 집합을 A의 스펙트럼이라고 부릅니다. 그리고 A가 대칭 행렬일 때, 다음의 성질을 따릅니다.

a. A가 n개의 고유치를 갖고 있으면 multiplicity를 계산합니다.
b. 각 고유치에 해당하는 고유공간의 차원은 고유치의 multiplicity와 동일합니다.
c. 고유공간은 서로 직교합니다. 서로 다른 고유치에 해당하는 고유벡터도 직교합니다.
d. A는 orthogonally diagonalizable 합니다.
스펙트럼 분해(Spectral Decomposition)
스펙트럼 분해(Spectral Decomposition)는 행렬 A를 eigenvalue(spectrum)으로 표현되는 조각들로 분해하는 것입니다.
어떻게 분해하는지 알아보도록 하겠습니다.
행렬 A가 orthogonally diagonalizable하다고 가정하고, 다음과 같이 표현할 수 있습니다.

위 수식을 다음과 같이 표현할 수 있습니다.

A를 위와 같이 표현한 것을 A의 스펙트럼 분해(spectral decomposition)이라고 합니다. 그리고 각 요소 $u_ku_k^T$는 rank가 1인 nxn 행렬입니다. rank=1은 column space의 dim이 1을 의미합니다.
그리고 각 행렬 $u_ju_k^T$는 투영 행렬(projection matrix)입니다. 이는 ch.5에서 배웠던 내용입니다.
스펙트럼 분해 예시 문제
orthogonal diagonalizable한 행렬 A를 스펙트럼 분해하는 문제입니다.
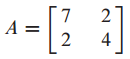
(1) 행렬 A를 직교 대각화(orthogonal diagonalization) 합니다.

(2) P의 행렬을 $u_1, u_2$로 표기합니다.

이처럼 간단히 스펙트럼 분해를 할 수 있습니다.
위 식이 진짜 A를 만족하는지 확인해보겠습니다.


읽어주셔서 감사합니다. 다음 포스팅에서는 Quadratic form에 대해 공부해보도록 하겠습니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.3 구속 최적화(Constrained Optimization) (0) | 2021.02.17 |
|---|---|
| [선형대수학] 6.2 이차 형식(Quadratic Forms) (7) | 2021.02.14 |
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |
| [선형대수학] 5.4 그람슈미트 과정과 QR 분해(Gram-Schmidt process and QR factorization) (1) | 2020.12.27 |
| [선형대수학] 5.3 정사영(Orthogonal Projections) (2) | 2020.12.27 |