David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

6.3 구속 최적화(Constrained Optimization)
구속 최적화는 이차 형식(Qudratic Form)에 제약 조건을 준것입니다.
이차 형식의 최대값과 최소값을 전체 영역에서 찾는 것이 아니라 제약조건 내에서 찾는 것입니다.
이차 형식에 다음과 같은 제약 조건을 줍니다.
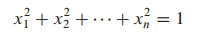
이는 Q(x) = $x^TAx$에서 $x^Tx$=1 을 의미합니다.
예시 문제
이차 형식과 제약 조건이 주어지고 최대값과 최소값을 찾는 문제입니다.
이차 형식

제약 조건

$x^2_2$와 $x^2_3$은 nonnegative이므로 다음이 성립합니다.
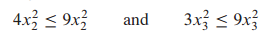
따라서 다음과 같이 됩니다.
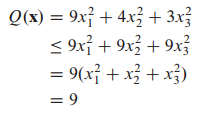
$x^Tx$ = 1 이라는 제약조건 때문에 Q(x) 최대값은 9를 초과할 수 없습니다.
따라서 x = (1, 0, 0)일 때, Q(x)=9가 되고 9가 최대값이 됩니다.
최소값은 다음과 같이 찾을 수 있습니다.


Q(x)은 제약조건 하에 3 미만의 값을 가질 수 없으므로 x=(0, 0, 1)일 때, Q(x) = 3이 최소값이 됩니다.
위 예제에서 이차 형식의 행렬(A)의 고유값은 9, 4, 3을 갖습니다. (이전 포스팅에서 살펴본 내용입니다.)
고유값의 최대값과 최소값은 제약 조건하의 이차 형식의 최대값과 최소값이 동일합니다.
구속조건 최적화를 시각적으로 확인해 보겠습니다.
이차 형식의 행렬 A가 다음과 같이 주어졌을 때, 이차형식과 구속 조건하의 이차 형식을 시각화한 그림입니다.
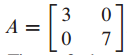

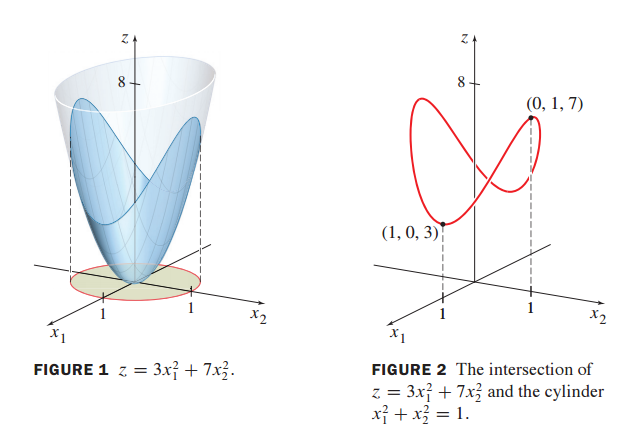
z축이 Q(x)를 나타냅니다.
그림 1의 이차형식에 제약 조건을 가한 것이 그림 2 입니다.
제약 조건하의 최대값과 최소값을 쉽게 확인할 수 있습니다.
이론 1
위 내용을 정리한 이론 입니다.

A가 대칭 행렬이고 M은 A의 가장 큰 고유값, m은 A의 가장 작은 고유값이라고 표기하겠습니다.
x가 M에 해당하는 unit 고유벡터일때, 이차 형식의 값은 M입니다.
x가 m에 해당하는 unit 고유벡터일때, 이차 형식의 값은 m입니다.
예시 문제
행렬 A가 주어졌을 때, 이차 형식 $x^TAx$의 최대값찾고 그에 해당하는 unit 고유벡터를 찾는 문제입니다.
이차 형식에 $x^TAx$=1 구속조건이 존재합니다.

이차 형식의 최대값은 A행렬의 가장 큰 고유값과 같습니다.
특성 방정식을 이용해 A의 최대 고유값을 찾은 뒤에 각각의 고유값에 해당하는 고유벡터를 찾고 정규화를 해주면 unit 고유벡터를 찾을 수 있습니다.

최대 고유값은 6이므로 이차 형식의 최대값은 6입니다.
고유값 6에 해당하는 고유벡터는 다음과 같습니다.

여기에 정규화를 취하면 다음과 같습니다.
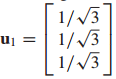
이것이 unit 고유 벡터가 됩니다.
이론 2
이론 2는 이차 형식에 제약 조건을 추가한 것입니다.

A행렬의 최대 고유값에 해당하는 유닛 고유벡터가 $u_1$이었습니다.
$x^Tu_1$=0 이라는 조건은 $x_1$ = 0을 의미합니다.
이 경우에 두 번째로 큰 고유값이 이차 형식의 최대값이 됩니다.
이론 3
이론 3은 이론 2번을 확장한 것입니다.
즉, 제약 조건을 확장한 것이라고 생각해볼 수 있습니다.

제약 조건이 추가적으로 $x^Tu_{k-1}$까지 주어졌을 때, x가 $u_k$이면 이차 형식은 최대값이 됩니다.
그리고 그 최대값은 $u_k$에 해당하는 고유값이 됩니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.5 Reduced SVD, 유사역행렬(Pseudoinverse) (0) | 2021.03.03 |
|---|---|
| [선형대수학] 6.4 특이값 분해(SVD, Singular Value Decomposition) (1) | 2021.03.03 |
| [선형대수학] 6.2 이차 형식(Quadratic Forms) (7) | 2021.02.14 |
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |