David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

Reduced SVD
A 행렬을 SVD하면 다음과 같이 됩니다.

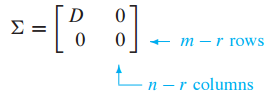
위 행렬은 대각 행렬인 D를 포함하는데, D 행렬은 대각 요소가 특이값(singular value)로 이루어진 rxr 크기의 행렬입니다. r행,열 까지는 특이값으로 이루어져있고, r+1 행과 r+1 열부터는 값이 0이 됩니다. U와 V가 r+1행, r+1열부터는 0과 곱해져 0이 되는 것입니다.
어차피 r을 초과하는 인덱스는 0과 곱해져 0이 되므로 U와 V행렬을 r까지만 표기한것이 Reduced SVD입니다.
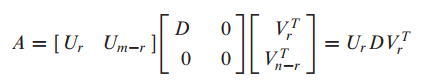
유사역행렬(Pseudo inverse)
유사역행렬은 $A^+$를 정의해서 최소제곱법(leaset-square sulotuon)을 구하는데 이용합니다.
$A^+$를 다음과 같이 정의합니다.
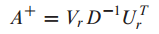
Ax=b를 풀고자 할때, x를 다음과 같이 정의합니다.

$\hat{x}$의 양변에 A를 곱해 방정식을 풀면 다음과 같이 됩니다. A는 reduced SVD로 분해한 값을 대입합니다.
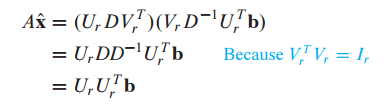
$V^T_r$은 orthonormal matrix이므로 $V^T_rV_r = I_r$이 됩니다.
$D^{-1} = D^T$이므로 $DD^-1$ = I가 됩니다.
따라서 다음의 식만 남게됩니다.
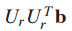
$U_r$은 ColA를 span하는 정규직교기저(orthonormal basis)입니다.
이는 정사영(orthogonal projection)에서 배웠던 projection 식과 동일합니다.

b를 ColA에 projection 한것입니다.
$A \hat{x}$는 b를 colA에 projection한 것이 되고, $\hat{x}$는 Ax=b의 최소제곱법이 됩니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.4 특이값 분해(SVD, Singular Value Decomposition) (1) | 2021.03.03 |
|---|---|
| [선형대수학] 6.3 구속 최적화(Constrained Optimization) (0) | 2021.02.17 |
| [선형대수학] 6.2 이차 형식(Quadratic Forms) (7) | 2021.02.14 |
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |