David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

6.4 특이값 분해(SVD, Singular Value Decomposition)
6.1 대칭행렬의 대각화에서 배웠던 대각화 이론은 많은 분야에서 적용할 수 있습니다. 하지만, 모든 행렬이 $A=PDP^{-1}$로 분해되지 않습니다. D가 대각행렬이기 때문에 A는 m x m 행렬이어야지 대각화를 할 수 있었습니다.
특이값 분해($A=QDP^{-1}$)는 행렬의 크기(m x n)와 상관없이 대각화가 가능합니다.
m x n 행렬의 특이값(The Singular Values of an m x n Matrix)
m x n 크기의 행렬 A의 특이값(singular values)은 $A^TA$의 고유값(eigen values)에 루트를 씌운 값입니다. 그리고 $\sigma$로 표기합니다.
$A^TA$는 n x n 크기의 대각행렬(symmetric matrix)입니다. 그리고 대각 행렬은 대각 요소가 동일하므로 전치를 해도 원래 행렬이 되는 특징과 직교 대각화(orthogonally diagonalizable)가 가능합니다.
$A^TA$ 행렬을 직교 대각화한 뒤에, 고유값을 구합니다. 그리고 그 고유값에 루트를 취하면 A 행렬의 특이값을 구할 수 있습니다.
그리고 A의 특이값(singular value)은 $Av_1, Av_2, ... , Av_n$ 벡터의 길이이며 $A^TA$의 고유값에 루트를 취해 구합니다. v는 $A^TA$의 고유 벡터입니다.
예시 문제
행렬 A가 주어지고, Ax 길이가 최대가 되는 유닛 벡터 x와 A의 특이값을 찾는 문제입니다. 구속조건은 x 길이가 1입니다.

A의 특이값은 $A^TA$의 고유값을 찾은 뒤에 루트를 씌워주면 됩니다.

특성 방정식으로 고유값을 찾으면, 아래와 같이 됩니다.

여기에 루트를 씌우면 A행렬의 특이값이 됩니다.

특이값을 찾았으므로, 이제 Ax의 길이가 최대가 되는 유닛 벡터 x를 찾겠습니다.
가장 큰 고유값에 해당하는 고유벡터를 찾고 정규화를 하면 됩니다.

$A^TA$가 대칭행렬이므로 고유 벡터인 v는 정규 직교(orthonormal) 벡터입니다.
$Av_1, Av_2, ~, Av_n$은 서로 직교합니다.
Av의 길이는 A 행렬의 특이값이고 r개가 존재합니다.
따라서 i가 1~r인 경우에 $Av_i$는 non zero이고, i가 r보다 커지면 Av는 0이 됩니다. 특이값이 r개가 존재하기 때문입니다.


이 특성를 이용하여 특이값 분해를 할 수 있습니다.
특이값 분해(SVD, Singular Value Decomposition)
SVD를 배우기 전에, 행렬 하나를 정의하겠습니다.

이 행렬은 크기가 m x n이고, r x r크기의 대각 요소가 특이값인 대각 행렬 D를 포함합니다. r은 m이나 n을 초과하지 않습니다.

특이값 분해는 행렬 A를 다음과 같이 분해하는 것입니다.

U는 {$Av_1, ... , Av_r$}을 정규화 한 {$u_1, ... u_r$} 벡터가 열들로 이루어진 행렬입니다. 그리고 A의 left singular vector로 부릅니다.


V는 $A^TA$의 정규직교 고유벡터(orthonormal eigenvector)가 열들로 이루어진 행렬입니다. A의 right singular vector로 부릅니다.

예시 문제
주어진 행렬을 특이값 분해 하는 문제입니다.
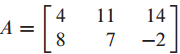
$A^TA$를 직교 대각화(orthogonal diagonalization) 하여, 고유값과 정규직교 고유벡터를 찾습니다.
고유값에 루트를 씌우면 A의 특이값이 되고, 고유벡터로 행렬 V를 만들 수 있습니다.


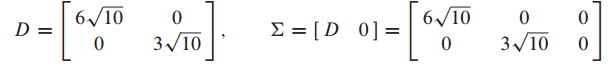
이제 U행렬을 만듭니다. U 행렬은 Av에 정규화를 한 벡터들이 열을 구성하고 있습니다.


Bases for Fundamental Subspaces
SVD를 구성하는 행렬이 subspace와 어떤 관계가 있는지 살펴보겠습니다.
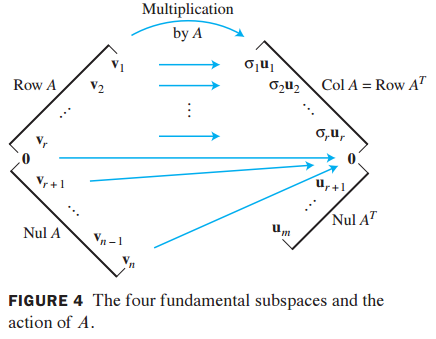
A의 left singular vector인 {$u_1, ... ,u_r$}은 ColA의 정규직교 기저(orthonormal basis)입니다.
CoA의 perpendicular는 Nul$A^T$이며, {$u_{r+1}, ... ,u_m$}가 Nul$A^T$의 정규직교 기저입니다.
A의 right singular vector인 {$v_1, ... , v_r$}는 RowA의 정규직교기저이고,
{$v_{r+1}, ... ,v_m$}은 NulA의 정규직교 기저입니다.
이를 그림으로 표현하면 다음과 같습니다.
다음 포스팅에서는 Reduced SVD와 Pseudoinverse에 대해 공부해보겠습니다! 감사합니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.5 Reduced SVD, 유사역행렬(Pseudoinverse) (0) | 2021.03.03 |
|---|---|
| [선형대수학] 6.3 구속 최적화(Constrained Optimization) (0) | 2021.02.17 |
| [선형대수학] 6.2 이차 형식(Quadratic Forms) (7) | 2021.02.14 |
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |