David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

오랜만에 올려보는 선형대수학 포스팅입니다.
이차 형식(Quadratic forms)
이차 형식(Quadratic form)은 다음과 같이 정의됩니다.

A는 nxn 크기의 대칭 행렬(symmetric matrix)이고 이차 형식의 행렬(the matrix of the quadratic form)이라고 불립니다.
대칭 행렬의 특징은 이전 포스팅에서 공부했었습니다. 간단히 요약하면, 대칭 행렬을 P와 D로 분해하면 P의 column이 A의 eigen vector로 이루어져 있고, 각 vector는 서로 직교한다는 것이었습니다. 그리고 이를 직교 대각화 가능이라고 불렀습니다.
이차 형식의 몇 가지 예제를 살펴보겠습니다.
예제 1
x가 다음과 같이 주어졌을 때, 이차 형식 $x^TAx$를 구하는 문제입니다.

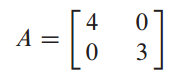

A의 대각 요소가 x1, x2의 weight가 되었습니다.
예제 2
예제 2에서는 A가 다음과 같이 주어졌습니다.


예제 1번과 예제 2번의 차이는 A행렬에 -2 요소가 생겼습니다.
그리고 -2 요소에 의해 cross-product term인 $-4x_1x_2$ 가 생겼습니다.
이 -2 요소 때문에 계산이 복잡해졌습니다.
예제 3
주어진 이차 형식을 $x^TAx$ 형식으로 작성하는 문제입니다.
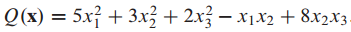

이차 형식이 cross-product term을 갖고 있지 않으면 쉽게 사용할 수 있습니다.
그리고 cross-product term은 변수를 변경하여 제거할 수 있습니다.
이차 형식에서 변수 변경(Change of Variable in a Quadratic Form)
이차 형식에서 변수를 변경하여 cross-product term을 제거할 수 있습니다. cross-product term이 제거되면 이차 형식을 좀 더 쉽게 사용할 수 있습니다.
x를 다음과 같이 표현합니다.


P는 A행렬의 eigen vector입니다. A 행렬이 대칭 행렬이면, P의 각 column은 직교합니다.
그리고 이 x=Py를 쿼드라틱 폼에 대입합니다.

$P^TAP$는 대각화 이론에 의해 D가 됩니다. 따라서 최종적으로 다음과 같이 변경됩니다.

D는 D의 대각 요소가 A 행렬의 eigen value로 이루어진 대각 행렬입니다.
이차 형식이 $y^TDy$로 변경되어 cross-product term이 제거됩니다.
예시 문제 1
주어진 A행렬을 변수 변경하는 문제입니다.

A 행렬에 -4 요소는 cross-product term 입니다. 이 term을 변수 변경을 통해 없애는 문제입니다.
A 행렬은 대칭 행렬이므로 직교 대각화(orthogonally diagonalize) 할 수 있습니다.
특성 방정식을 이용해 고유값과 고유벡터를 찾습니다.
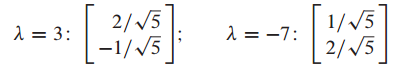
P와 D행렬을 만듭니다.



이제 x를 다음과 같이 변경합니다.
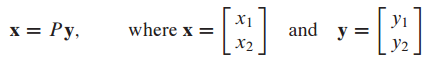
위 x를 이차 형식에 대입합니다.

cross-product term이 제거되었습니다.
변수 변경을 시각화하면 다음과 같습니다.

주축 이론(The Principal Axes Theorem)

위에서 배운 것을 이론화한 것입니다.
A행렬이 nxn 대칭 행렬이라고 가정하겠습니다. 이차 형식 Q(x) = $x^TAx$에서 x=Py를 대입해 $y^TDy$로 변경하면 cross-product term이 사라집니다.
A행렬의 eigenvetor로 이루어진 P행렬을 이차형식의 주축(principal axes)라고 부릅니다.
주축의 기하학적 시점(A Geometric View of Principal Axes)
시각적인 관점으로 보면 주축이 편리한 점이 있다는 것을 확인할 수 있습니다.
이차 형식에서 cross-product term이 없는 경우 타원과 포물선은 다음과 같습니다.

cross-product term이 있는 경우 타원과 포물선입니다.

주축(y1, y2)을 기준으로 일반적인 타원과 포물선을 그린 것입니다.
cross-product term을 없애고 주축을 기준으로 원이나 포물선을 그리면 쉽게 도형을 그릴 수 있습니다.
이차 형식 분류하기(Classifying Quadratic form)
이차 형식을 용어적으로 몇 가지로 구분할 수 있습니다.
1. positive definite if Q(x) > 0 for all x != 0
아래 그림에서 x3 = Q(x)를 의미합니다.
x=0을 제외한 모든 Q(x)가 양수이면 positive definite 라고 합니다.

2. negative definite of Q(x) < 0 for all x != 0
x=0을 제외한 모든 Q(x)가 음수이면 negative definite 입니다.

3. indefinite if Q(x) assumes both positive and negative values
Q(x)가 양수와 음수 모두 지니고 있으면 indefinite 입니다.

4. positive semidefinite if Q(x) >= 0 for all x
모든 x에 대해 Q(x)가 0이상이면 positive semidefinite 입니다.
5. negative semidefinite if Q(x) <= 0 for all x
모든 x에 대해 Q(x)가 0 이하이면 negative semidefinite 입니다.
이차 형식과 고유치(Quadratic Forms and Eigenvalues)

A 행렬의 고유치를 보고 이차 형식을 구분할 수 있습니다.
a. A의 고유치가 모두 양수이면 positive definite
b. A의 고유치가 모두 음수이면 negative definite
c. A의 고유치가 양수와 음수 모두 지니고 있으면 indefinite 입니다.
증명
이차 형식을 변수 변경하여 표현하면 다음과 같습니다.

$y^2_n$은 제곱 형태이므로 모두 양수입니다.
따라서 $\lambda$(고유치)에 의해 이차 형식의 부호가 결정됩니다.
예시 문제 1
주어진 이차 형식을 구분하는 문제입니다.

A 행렬의 고유치를 확인하면 알 수 있습니다.

특성 방정식으로 A 행렬의 고유치를 구하면 5, 2, -1 입니다.
양수와 음수를 지니고 있으므로 이차 형식은 indefinite quadratic form으로 구분됩니다.
고유치를 보는것 이외에 이차 형식을 구분하는 방법이 있습니다.
cholesky factorization으로 이차 형식을 구분할 수 있습니다.
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.4 특이값 분해(SVD, Singular Value Decomposition) (1) | 2021.03.03 |
|---|---|
| [선형대수학] 6.3 구속 최적화(Constrained Optimization) (0) | 2021.02.17 |
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |
| [선형대수학] 5.4 그람슈미트 과정과 QR 분해(Gram-Schmidt process and QR factorization) (1) | 2020.12.27 |