David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

드디어 5장의 마지막 부분인 최소자승법(Least-Squares Problems)에 대해 공부해 보겠습니다!
선형대수학 공부를 처음 시작할 때 언제 다 할 수 있을까라는 막막했는데, 꾸준히 해나가니까 끝이 보이네요ㅎㅎ
항상 꾸준히 하는것이 중요한 것 같습니다.
Ax=b 문제를 풀 때 해가 없는 경우가 대부분입니다.
현실의 문제에는 여러가지 오차가 포함되어 있기 때문입니다.
이런 경우 b와 제일 근접한 x를 찾게됩니다.
이때 이용하는 방법이 최소자승법 입니다.
1. 최소자승법의 해(Least-Squares Solution)

b-Ax를 가장 작게하는 x가 $\hat{x}$이며, 이것이 least-squares의 solution 입니다.

x는 Col A의 space에 존재합니다.
mxn 크기 행렬 A의 column이 선형 독립(linearly independent)란 말이 없으므로 dim Col A $\leq$ n이 성립합니다.
b와 가장 근접한 x를 찾았다고 가정하고 $\hat{x}$라고 표현하겠습니다.
그러면 A$\hat{x}$ = $\hat{b}$로 표현할 수 있습니다.

$\hat{b}$는 A의 Col A에 존재하며 A$\hat{x}$=$\hat{b}$는 consistent 합니다. 이는 해가 존재한다는 의미입니다.
만약 자유 변수(free variable)을 지니게 되면 해가 무수히 많아집니다.
A$\hat{x}$ = $\hat{b}$에서 b-$\hat{b}$는 Col A와 직교(orthogonal)합니다.
b-$\hat{b}$가 A의 각 column에 직교하므로 A$\cdot(b-A\hat{x})$는 0이 됩니다.
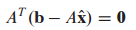
위 식을 풀어쓰면 다음과 같이 됩니다.

위 식은 x가 least-squares solution of Ax=b 일 때 만족합니다.

위 식을 정규 방정식(normal equation)이라고 합니다.
$\hat{x}$를 찾기 위해 정규 방정식을 풉니다.
2. 이론 13

정규 방정식의 해 nonempty 집합은 Ax=b의 least-squares solution과 일치합니다.
여기서 least-squares solution은 $\hat{x}$를 의미합니다.
$\hat{x}$를 찾고 싶으면 정규 방정식(normal equation)을 풀면 됩니다.
증명
$b-A\hat{x}$는 A의 column set Col A와 직교합니다. 이는 위에서 설명한 내용입니다.
그리고 $A\hat{x}$는 Col A에 존재합니다.
이 두개를 이용해서 b를 저번 포스팅에서 공부하였던 직교 분해(orthogonal decomposition)로 표현할 수 있습니다.

b의 decomposition은 유일하다는 것을 배웠습니다.
$A\hat{x}$는 b를 Col A에 정사영(orthogonal projection)한 것이고 ($b-A\hat{x}$)는 b의 직교 요소 입니다.
따라서 $A\hat{x} = \hat{b}$에서 $\hat{x}$는 least-squares solution 입니다.
3. 최소자승 에러(Least-Squares Error)
b에 근사치로서 $A\hat{x}$를 만들기 위해 최소자승해 $\hat{x}$가 사용되면, b와 $A\hat{x}$ 거리는 근사치의 최소자승 에러(Least-Squares Error)라고 합니다.
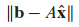
4. 이론 14

a. Ax=b는 b에 대한 최소자승해는 유일합니다.
b. A의 columns는 선형 독립입니다.
c. $A^TA$는 역행렬이 존재합니다.
위 3가지 조건을 충족하면 다음이 성립합니다.
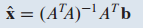
5. 이론 15

저번 포스팅에서 A가 선형 독립 column으로 이루어져 있으면 A를 QR로 분해할 수 있다는 것을 배웠습니다.
여기서 Q는 orthonomal column으로 이루어진 행렬이고, R은 upper triangular matrix 입니다.
A가 QR 분해가 가능한 행렬이면 최소자승해는 다음과 같이 구할 수 있습니다.
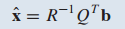
증명
$A\hat{x}=b$에 A=QR과 위 식을 대입하면 다음과 같이 됩니다.

Q는 A의 orthonormal basis입니다.
$QQ^T$는 1이 되어 $A\hat{x}$=b를 만족하게 됩니다.
$\hat{x}$를 구할 때,

이 식보다는
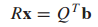
이 식을 많이 이용합니다.
R의 역행렬을 계산하기 위해 많은 연산이 필요하기 때문입니다.
예시 문제
Ax=b의 최소자승해를 구하는 문제입니다.
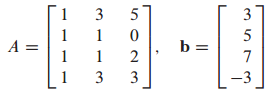
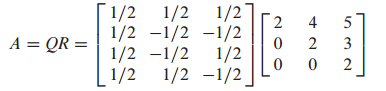

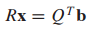
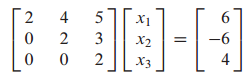
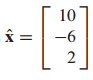
'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 6.2 이차 형식(Quadratic Forms) (7) | 2021.02.14 |
|---|---|
| [선형대수학] 6.1 대칭 행렬의 대각화(Diagonalization of symmetric matric) (6) | 2021.01.18 |
| [선형대수학] 5.4 그람슈미트 과정과 QR 분해(Gram-Schmidt process and QR factorization) (1) | 2020.12.27 |
| [선형대수학] 5.3 정사영(Orthogonal Projections) (2) | 2020.12.27 |
| [선형대수학] 5.2 직교 집합(Orthogonal Sets)과 정사영(Orthogonal Projection) (1) | 2020.12.23 |