저번 포스팅에서 정사영이 무엇인지 간략하게 알아보았습니다.
이번에는 정사영에 대해 자세히 배워보도록 하겠습니다.
저번 시간에 배운 내용을 복습해보겠습니다.
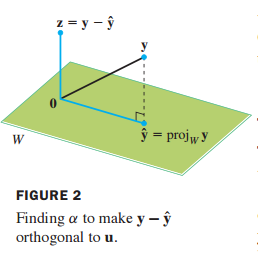
벡터 y와 부분공간 W가 주어졌을 때, y를 서로 직교하는 두 개의 벡터 합으로 분해할 수 있다고 배웠습니다.
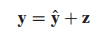
여기서 $\hat{y}$는 W 부분공간 안에 있으며 다음과 같이 구할 수 있습니다.

1. 이론 8 직교 분해 이론(The Orthogonal Decomposition Theorem)

벡터 y를 두 개의 벡터로 분해(decomposition)할 수 있으며 $\hat{y}$는 W 부분 공간안에 존재하고 z는 $W^{\perp}$에 존재합니다.
만약 {$u_1, ... ,u_p$}가 W의 직교 기저(orthogonal basis) 이면 $\hat{y}$는 u의 선형 결합(linear combination)으로 표현되고 각각의 가중치(weight)는 다음과 같이 표현할 수 있습니다.

그리고 z는 $\hat{y}$에 직교하며 y-$\hat{y}$로 나타낼 수 있습니다.
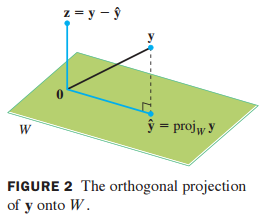
만약 y가 W에 존재할때, y를 W에 projection하면 y가 나옵니다.
예시 문제
W의 직교 기저인 $u_1, u_2$와 y가 주어졌을 때, y를 W에 있는 벡터와 W와 직교하는 벡터의 합으로 분해하는 문제입니다.


문제에서 묻는 것은 y를 아래 식으로 표현하는 것입니다.

$\hat{y}$는 다음과 같이 구할 수 있습니다.
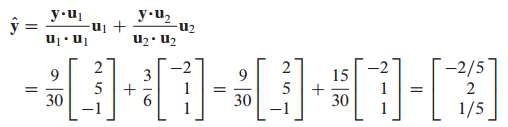
그리고 z는 다음과 같이 구할 수 있습니다.

따라서 정답은 다음과 같이 됩니다.

2. 정사영의 기하학적 해석(A geometric interpretation of the Orthogonal Projection)
y를 2차원 평면 W에 projection 하는 것을 생각해 보겠습니다.
평면 W는 직교 기저 $u_1, u_2$가 span 합니다.
y를 평면 W에 projection 하는 방법은 각각의 직교 기저에 projection 한 것을 더해주면 됩니다.
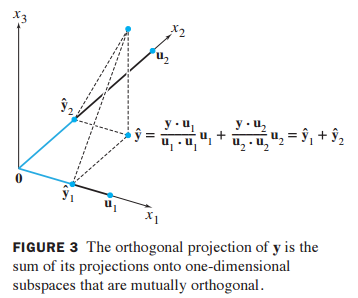
$\hat{y_1}$ 은 $u_1$에 projection 한 것이고
$\hat{y_2}$ 는 $u_2$에 projection 한 것입니다.
3. 이론 9. 최고 근사 이론(The best approximation theorem)

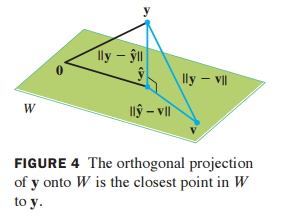
특정 벡터 y와 부분 공간 W 간의 제일 짧은 거리를 구하는 이론입니다.
y를 W에 projection 한 $\hat{y}$가 y와 W에 제일 가까운 곳입니다.
증명
$\hat{y}$과 다른 W안에 있는 벡터 v를 생각해보겠습니다.
$\hat{y}$와 v 둘 다 W안에 있게 되고 $\hat{y}$ - v도 W안에 있게 됩니다.
직교 분해 이론에 의해 y-$\hat{y}$는 W에 직교하게 됩니다.
마찬가지로 $\hat{y}$-v도 W에 있으므로 y-$\hat{y}$와 직교합니다.
따라서 다음과 같이 표현할 수 있습니다.
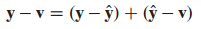
위 식에서 피타고라스의 정리에 의해 다음과 같이 표현됩니다.
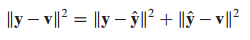
따라서 다음 식이 성립하게 됩니다.

예제 문제
W는 span{$u_1, u_2$}이고 $u_1$ = (5, -2, 1), $u_2$ = (1, 2, -1), y = (-1, -5, 1-)으로 주어졌을 때 y와 W의 거리를 구하는 문제입니다.



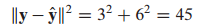
따라서 W와 y의 거리는 다음과 같이 구할 수 있습니다.

4. 이론 10

{$u_1, ... ,u_p$}가 W에 대한 정규 직교 기저(orthonomal basis)일 때, y를 W에 projection 한 것은 다음과 같이 표현할 수 있습니다.
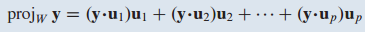
$u\cdot u$가 생략되었는데 이는 1이기 때문입니다.
만약 U를 [$u_1, ... ,u_p$]로 표현한다면 y를 W에 projection 한 것은 다음과 같이 표현할 수 있습니다.

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 5.5 최소자승법(Least-Squares Problems) (8) | 2020.12.28 |
|---|---|
| [선형대수학] 5.4 그람슈미트 과정과 QR 분해(Gram-Schmidt process and QR factorization) (1) | 2020.12.27 |
| [선형대수학] 5.2 직교 집합(Orthogonal Sets)과 정사영(Orthogonal Projection) (1) | 2020.12.23 |
| [선형대수학] 5.1 내적(Inner Product), 길이(Length) 그리고 직교성(Orthogonality) (0) | 2020.12.22 |
| [선형대수학] 4.4 고유벡터와 선형변환(Eigenvectors and Linear Transformation) (0) | 2020.12.08 |