이번 포스팅에서 내적(inner product), 길이(length), 직교성(orthogonality)에 대해 알아보도록 하겠습니다.
지금까지 Ax = b 형태의 방정식을 푸는 법을 배웠습니다. 하지만 실험 데이터로 수식을 세워 풀어보면 수식과 일치하는 경우가 거의 없습니다. 실험 데이터는 오차가 있을 수 밖에 없기 때문입니다. 이 경우에 b와 제일 가까이 있는 x를 찾아야 합니다. 이것이 제일 합리적인 방법입니다.
1. 내적(Inner Product)
직교성을 알아보기전에 먼저, 내적에 대해 알아보겠습니다.
동일한 $R^n$ 공간에서 두 개의 벡터가 주어졌습니다.
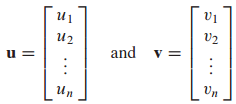
u와 v의 내적은 다음과 같이 정의됩니다.
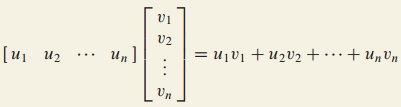
이는 $u^T$v를 의미합니다. 또한 두 벡터의 순서가 바뀌어도 됩니다.
두 벡터의 내적을 $u\cdot v$로 표현합니다.
예시 문제
두 벡터의 내적을 구하는 문제입니다.


이처럼 두 벡터의 순서가 바뀌어도 결과값은 동일하다는 것을 확인할 수 있습니다.

2. 이론 1(Theorem 1)
이론 1은 내적의 정의에 대한 이론입니다.
동일한 공간에서 벡터와 스칼라 C가 있을 때 다음 4개의 조건을 만족합니다.

d 조건은 동일한 벡터의 내적은 0보다 큽니다. 각 항목의 제곱이기 때문입니다. 만약 u$\cdot$u = 0 이면 u=0임을 의미합니다.
3. 벡터의 길이(Lengh of a Vector)

벡터의 길이는 동일한 벡터 두개를 내적하고 루트를 씌운 것과 동일합니다.
동일한 벡터를 내적을 하게 되면 각 항목이 제곱이 되는데, 이는 피타고라스 정리와 동일합니다.

벡터의 길이 llvll를 norm 이라고 합니다.
norm이 스칼라와 곱해졌을 때 다음의 성질을 만족합니다.

벡터의 길이가 1이면 이를 유닛 벡터(unit vector)라고 합니다.
llull = 1
또한 벡터 v가 주어졌을 때 각 항목을 norm으로 나누면 길이가 유닛 벡터가 됩니다.
이처럼 벡터에 1/norm을 곱하는 것을 normalizing 이라고 합니다.

normalizing을 하게 되면 v와 같은 방향을 가르키는 벡터이며 길이가 1이 됩니다.
예시 문제
벡터v가 주어졌을 때, v와 같은 방향을 나타내며 길이가 1인 유닛 벡터 u를 찾는 문제입니다



v의 norm을 구하고 norm을 v에 나눠주면 찾을 수 있습니다.
4. $R^n$ 공간에서의 거리(Distance in $R^n$)

두 벡터 차의 길이가 거리(distance)가 됩니다.
예시 문제 1
두 벡터가 다음과 같이 주어졌을 때 두 벡터 간의 거리를 구하는 문제입니다.

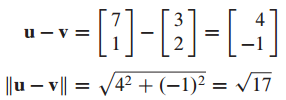

5. 직교 벡터(Orthogonal Vectors)
dist(u,-v), dist(u,v)이 같으려면 두 벡터가 직교해야 합니다.
이처럼 두 벡터가 직교인 경우 직교 벡터라고 합니다.
dist(u,-v)와 dist(u,v) 를 자세히 살펴보겠습니다.


두 거리가 동일하려면 다음과 같이 되어야 합니다.

이는 u와 v의 내적이 0이게 되면 성립합니다.

dist(u,-v)와 dist(u,v)가 동일하려면 u$\cdot$v =0이 성립해야 하고, 직각인 경우에 두 거리가 동일하므로 결국 u$\cdot$v=0이면, 두 벡터가 직교(orthogonal)인 것을 의미합니다.


6. 이론 2 피타고라스 정리(Theorem 2. Pythagorean Theorem)

두 벡터가 직교(orthogonal)이면 $\parallel u+v\parallel^2$ = $\parallel u\parallel^2 + \parallel v\parallel^2$가 성립합니다.

7. 직교여공관(Orthogonal Complements)

$R^3$ 공간에서 평면 W가 원점을 통과하고 원점을 통과하는 직선 L이 W와 직각이 되면 L에 있는 모든 벡터는 w와 직교합니다. 이는 L에 있는 임의의 벡터 z와 평면 W의 임의의 벡터 w의 내적은 0이 된다는 것을 의미합니다.
이처럼 z가 W에 존재하는 모든 벡터와 직교하면 z는 W에 직교한다고 말할 수 있습니다.
z가 W에 직교하는 것을 W의 직교 여공간이라고 부르며 다음과 같이 표기합니다.
그리고 수직(perpendicular)이라고 읽습니다.

위 그림에서 W와 L은 직교하므로 다음과 같이 표기할 수 있습니다.

추가적으로 0 벡터는 모든 벡터와의 내적이 0이므로 모든 벡터와 직교합니다.
예시 문제

만약 W가 $R^n$ 공간의 부분 공간이고, x가 W를 span하는 모든 벡터와 직교하면 x는 $W^\perp$ 안에 존재합니다.
또 $W^\perp$는 $R^n$ 공간의 부분 공간(subspace)입니다.
부분 공간의 조건은 3가지가 있습니다.
(1) 0 벡터를 포함해야 합니다.
(2) 스칼라 곱과 (3) 벡터 합에 닫혀 있어야 합니다.
x는 W의 임의의 벡터 u와 $W^\perp$의 임의의 벡터 cx와 세 가지 조건을 만족합니다.
u$\cdot$cx = cu$\cdot$x = 0 이 성립하므로 스칼라 곱에 닫혀있습니다.
u$\cdot$($z_1$+$z_2$) = u$\cdot z_1$ + u$\cdot z_2$ = 0 이 성립하므로 벡터 합에 닫혀있습니다.
0 벡터는 모든 벡터에 직교이고 $W^\perp$안에 존재하므로 세 가지 조건을 만족하게 됩니다.
8. 이론 3(Theorem3)

Nul A는 Ax=0을 만족하는 모든 x 집합을 의미합니다.
Row A는 A의 모든 row를 벡터로 만들어서 span 한 행 공간(row space)를 의미합니다.
Col A는 A의 모든 column을 벡터로 만들어서 span 한 열 공간(column space)를 의미합니다.
Row A의 수직(perpendicular)이 A의 null space가 됩니다.

David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다.

'수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 5.3 정사영(Orthogonal Projections) (2) | 2020.12.27 |
|---|---|
| [선형대수학] 5.2 직교 집합(Orthogonal Sets)과 정사영(Orthogonal Projection) (1) | 2020.12.23 |
| [선형대수학] 4.4 고유벡터와 선형변환(Eigenvectors and Linear Transformation) (0) | 2020.12.08 |
| [선형대수학] 4.3 대각화(Diagonalization), 행렬 대각화하기 (0) | 2020.12.07 |
| [선형대수학] 4.2 특성 방정식 - The Characteristic Equation - 유사도(similar), similar transformation (0) | 2020.12.05 |