딥러닝 공부방

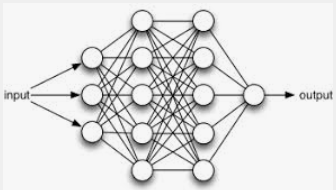
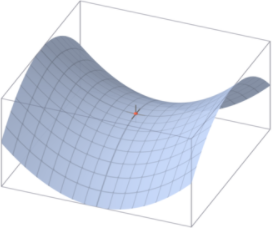
(밑바닥부터 시작하는 딥러닝, 사이토고키)를 바탕으로 제작하였습니다. 오차역전파법(4) - 오차역전파법을 사용한 학습 구현 이전의 포스팅에서는 역전파를 적용한 활성화함수(ReLu, Sigmoid) 계층, Affine 계층, Softmax-with-Loss 계층을 구현해 보았습니다. 이번 포스팅에서는 지금까지 구현한 계층을 조합해서 오차역전파법을 사용한 학습을 구현해보겠습니다. 7. 오차역전파법 구현하기 7.1 신경망 학습의 전체 그림 우선 신경망 학습의 전체 그림을 복습해보겠습니다. 다음은 신경망 학습의 순서입니다. 전체 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 합니다. 신경망 학습은 다음과 같이 4단계로 수행합니다. 1단계 ..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (3) - 학습 알고리즘 구현 지금까지 배운 내용을 이용해서 신경망 학습 알고리즘을 구현해보겠습니다. 5. 학습 알고리즘 구현하기 신경망 학습의 절차는 다음과 같습니다. 전체 신경망에는 적응 가능한 가중치와 편향이 있고, 이 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정을 '학습'이라 합니다. 신경망 학습은 다음과 같이 4단계로 수행합니다. 1단계 - 미니배치 훈련 데이터 중 일부를 무작위로 가져옵니다. 이렇게 선별한 데이터를 미니배치라 하며, 그 미니배치의 손실 함수 값을 줄이는 것이 목표입니다. 2단계 - 기울기 산출 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구합니다. 기울기는 손..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (2) - 기울기와 경사하강법 이전의 포스팅에서는 손실 함수와 수치 미분을 공부했습니다. 이번 포스팅에는 손실 함수의 기울기를 구하고 경사법으로 손실 함수 결과값이 최소가 되는 지점으로 가중치를 갱신시켜주는 방법에 대해 공부해보겠습니다. 4. 기울기 - Gradient 기울기는 모든 변수의 편미분을 벡터로 정리한 것을 의미합니다. $f$($x_0$, $x_1$) = $x_{0}^{2}$ + $x_{1}^{2}$ 이전의 포스팅에서는 $x_0$와 $x_1$의 편미분을 변수별로 따로 계산했습니다. 그럼 $x_0$와 $x_1$의 편미분을 동시에 계산하는 방법을 알아보겠습니다. 위 식에서 $x_0$ = 3, $x_1$ = 4 일때..

(밑바닥부터 시작하는 딥러닝, 사이토고키) 를 바탕으로 작성하였습니다. 신경망 학습 (1) - 손실 함수와 수치 미분 이번 포스팅의 주제는 신경망 학습입니다. 여기서 학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 자동으로 획득하는 것을 뜻합니다. 손실 함수를 소개합니다. 손실 함수는 신경망이 학습할 수 있도록 해주는 지표입니다. 이 손실 함수의 결과값을 가장 작게 만드는 가중치 매개변수를 찾는 것이 학습의 목표입니다. 경사법을 소개합니다. 손실 함수의 값을 가급적 작게 만드는 기법으로, 함수의 기울기를 활용합니다. 1. 데이터에서 학습한다. 신경망의 특징은 데이터를 보고 학습할 수 있다는 점입니다. 데이터에서 학습한다는 것은 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 뜻입니다. 신경..