딥러닝 공부방

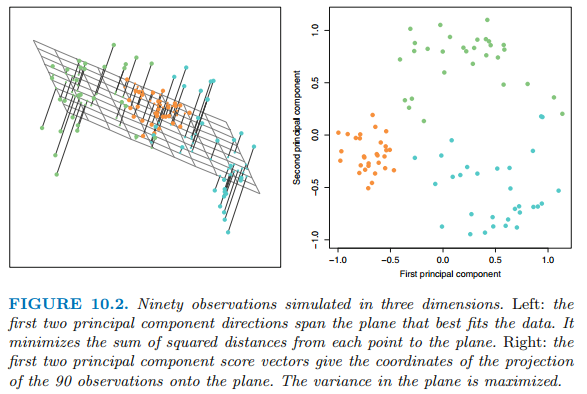
많은 수의 상관관계를 지닌 변수들이 존재하는 경우에 주성분 요소(Pricipal components)들은 적은 수로 변수들을 요약합니다. 따라서 주성분 요소를 활용하여 회귀를 진행하면 variance가 낮은 통계 모델을 얻을 수 있습니다. 이번 포스팅에서 공부할 주성분 분석(PCA)은 주성분 요소들을 계산하는 과정이며 주성분 요소들을 연속적으로 사용하여 데이터를 이해하는 과정입니다. 주성분 분석은 지도학습 문제에 사용하기 위한 파생 변수(derived variables)를 생성할 뿐만 아니라 데이터 시각화를 위한 도구로서 역할을 수행합니다. 주성분 분석(PCA, Principal Component Analysis) 탐색적 자료 분석(exploratory data analysis)로서 p개의 변수들에 대한..

주성분 회귀(Principal components regression, PCR) 주성분 회귀 기법은 p개의 변수를 m개의 변수로 축소하여 m개의 변수들로 선형회귀 모델을 fit합니다. m개의 변수는 주성분 요소(Z1, ..., Zm) 입니다. 주성분 요소는 데이터의 공분산 행렬에 SVD를 적용하여 구할 수 있습니다. PCR 기법은 설명변수 X1, ..., Xp를 가장 잘 나타내는 선형결합 또는 방향을 찾는 것입니다. 이러한 방향은 비지도 방식으로 식별되는데, 반응변수 Y가 주성분 방향을 결정하는데 이용되지 않기 때문입니다. 즉, 반응변수는 주성분을 찾는 것을 지도하지 않습니다. 따라서 PCR은 설명변수들을 가장 잘 설명하는 방향이 반응변수를 예측하는데 사용하기에도 가장 좋은 방향이 된다는 보장이 없습니다..

차원축소 방법 중 하나인 주성분 회귀를 알아보겠습니다. 차원축소 방법을 간단히 살펴보면 p개의 변수를 m개의 변수로 축소하여 bias를 증가시키고 variance를 감소합니다. 따라서 overfitting을 방지하는 효과가 있습니다. 주성분 회귀(Principal Components Regression) 주성분분석(PCA, Principal Components Analysis)는 변수의 큰 집합으로부터 저차원의 특징을 유도하기 위한 유명한 방법입니다. PCA는 비지도학습의 방법이며, 여기서는 회귀를 위한 차원축소 방법으로서 PCA를 사용하는 것을 살펴보겠습니다. 주성분 회귀를 알아보기 전에 주성분분석을 잠깐 살펴보겠습니다. 주성분분석 개요(An Overview of Principal Components ..