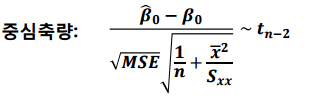딥러닝 공부방

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 절편 $\beta_0$ 에 대한 통계적 추론 회귀계수 중 절편에 해당하는 $\beta_0$의 중심축량과 구간추정에 대해 알아보겠습니다. 1. $\hat{\beta_0} = \overline{Y} - \hat{\beta_1}\overline{x}$의 역할 x가 0일 때 E(Y)의 값이 $\beta_0$ 입니다. 최소제곱법 추정으로 $\beta_0$ 추정과정을 알아보겠습니다. D를 $b_0$으로 미분함으로써 최소로하는 $b_1$과 $b_0$을 찾습니다. 추정한 $b_1, b_0$를 $\hat{b_1}, $\hat{b_0}$으로 표현합니다. $\beta_0$가 없는 모형에서의 잔차 합은 0이 되지 않을 수 있습니다. $b_0$이 0..

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 회귀계수(기울기)에 대한 통계적 추론 회귀계수 중 기울기에 해당하는 $\beta_1$의 중심축량, 구간추정, 가설검정에 대해 알아보겠습니다. 1. 기울기 $\beta_1$에 대한 추론 $\hat{\beta_1}$은 $\beta_1$의 추정값입니다. $\hat{\beta_1} = S_{xY}/S_{xx}$의 통계적 성질은 다음과 같습니다. $\hat{\beta_1}$의 기댓값은 다음과 같이 구할 수 있습니다. $\hat{\beta_1}$의 분산은 다음과 같습니다. $\hat{\beta_1}$의 기댓값과 분산을 구했으므로 $\hat{\beta_1}$는 다음과 같이 가정할 수 있습니다. 이를 표준화하면 중심축량을 구할 수 있습니다...

여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 저번 포스팅에서는 다변량 자료의 관계를 파악하는 방법인 산점도와 상관분석에 대해 공부해보았습니다. 이번에는 수치변수들 간 인과관계를 설명하기 위한 대표적인 통계모형인 회귀모형을 알아보겠습니다. 다변량 자료에서 주요 관심사 다변량 자료에서 주요 관심사는 변수들 간의 관계입니다. 1. 산점도와 상관분석으로 분석 가능한 관심사 (1) 변수들 간 관계가 있는가? (2) 있다면 어떤 관계가 있는가? (3) 관계가 어느 정도 되는가? 위 세 개의 관심사는 산점도와 상관분석을 통해 직선관계를 파악하여 분석할 수 있습니다. 산점도와 상관분석은 직선관계만 파악할 수 있습니다. 2. 회귀모형으로 분석 가능한 관심사 (1) 관계를 식으로 표시할 ..