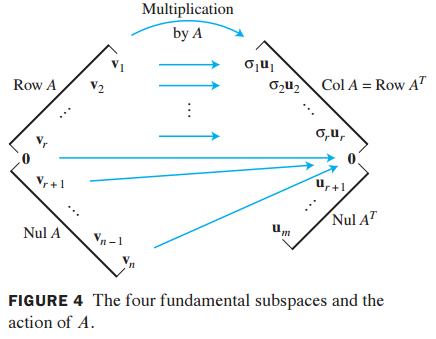
David C.Lay 의 Linear algebra and its application를 공부하면서 정리해보았습니다. 감사합니다. Reduced SVD A 행렬을 SVD하면 다음과 같이 됩니다. 위 행렬은 대각 행렬인 D를 포함하는데, D 행렬은 대각 요소가 특이값(singular value)로 이루어진 rxr 크기의 행렬입니다. r행,열 까지는 특이값으로 이루어져있고, r+1 행과 r+1 열부터는 값이 0이 됩니다. U와 V가 r+1행, r+1열부터는 0과 곱해져 0이 되는 것입니다. 어차피 r을 초과하는 인덱스는 0과 곱해져 0이 되므로 U와 V행렬을 r까지만 표기한것이 Reduced SVD입니다. 유사역행렬(Pseudo inverse) 유사역행렬은 $A^+$를 정의해서 최소제곱법(leaset-squ..