딥러닝 공부방

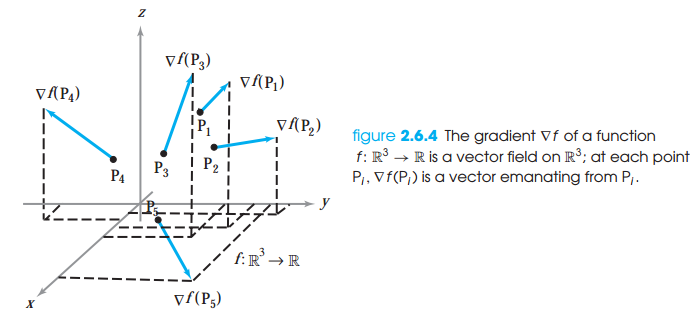
레벨 집합에서 그래디언트와 접평면(Gradients and Tangent Planes to Level Sets) level surface와 함수 f의 그래디언트 사이의 관계를 살펴보겠습니다. level surface는 함수 f의 값을 상수로 두고, 그 상수를 만족하는 점들의 집합을 나타낸 것입니다. 그래디언트는 함수 f의 값이 가장 빠르게 변화하는 방향을 나타냅니다. 이에반해 level surface는 f의 값이 전혀 변하지 않는 방향으로 놓여져 있습니다. level surface와 그래디언트는 직교합니다. 그래디언트와 level set은 수직이라는 것을 알았습니다. 그래디언트에 수직인 평면인 접평면을 정의하는 법을 알아보겠습니다. 그래디언트와 level surface는 수직이므로, 둘을 내적하면 0이 ..

선형근사(Linear Approximation) 다변수 함수 f가 충분히 매끄러울 때, 점(x_0, y_0)에서 함수의 그래프에 접하는 평면의 방정식을 구해보겠습니다. 수직이 아닌 평면의 방정식은 다음의 형태를 갖습니다. 만약 위 식이 함수의 그래프에 접하는 평면이라면 x와 y축을 따르는 기울기는 x와 y에 대한 함수 f의 변화율인 af/ay와 af/ax와 같아야 합니다. 따라서 a와 b는 다음과 같아야 합니다. 상수 c는 x=x0, y=y0인 경우에 z = f(x0, y0)이라는 사실로부터 구할 수 있습니다. 따라서 선형 근사(linear approximation)은 다음과 같이 구할 수 있습니다. 위 방정식은 만약 f가 충분히 smooth한 경우에 (x0, y0)에서 함수 f의 그래프에 접하는 평면의..