여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
단순선형회귀모형에서의 모수 추정
설명변수가 하나인 회귀모형에서 관측값과 회귀선과의 거리를 어떻게 표시하는지 알아보겠습니다.
최소제곱법을 이용한 회귀모수를 추정하는 방법을 알아보겠습니다.
1. 단순선형회귀모형 - Simple Linear Regression Model
단순선형회귀모형은 설명변수가 하나인 선형회귀모형을 의미합니다.
회귀모형 중에서 가장 간단한 형태입니다.

$x_i$를 소문자로 쓴 이유는 상수로 가정하기 때문입니다.
또한 $Y_i$ ~ iidN(0,$\sigma^2$)를 가정합니다.
$\epsilon$은 오차(error)를 의미하며 모형에서 설명이 안되는 부분입니다.
설명변수(x)는 조절 가능한 상수로 가정합니다.
광고비에 따른 판매량을 조사할 때 광고비는 회사에서 결정 가능합니다.
일조량에 따른 수확량은 일조량이 확률이지만 관측된 값으로 주어진 값으로 처리합니다.
설명변수가 여러개인 경우 다중회귀모형(multiple regresiion model)입니다.
회귀분석은 미지의 모수 절편 $\beta_0$, 기울기 $\beta_1$를 추정합니다.
$\beta_1$은 x를 한 단위 증가시길 때 Y의 증가량을 의미합니다.
$\beta_1$ = 0 이면 x가 Y에 영향을 주지 않는다는 것을 의미합니다.

$\beta_0 + \beta_1{x_i}$는 $x_i$일 때 $y_i$의 평균을 의미합니다.
2. 모수 추정
$\beta_0, \beta_1$의 추정값은 $b_0, b_1$로 표현합니다.
회귀선과의 거리를 이용해서 추정값을 구할 수 있습니다.

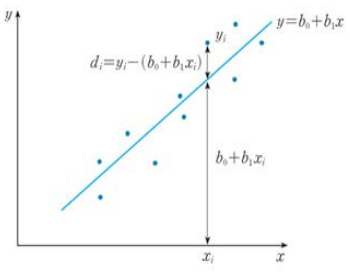
3. 추정된 직선이 좋은 직선인가 아닌가에 대한 기준
추정된 직선이 좋은 직선인가 아닌가에 대한 기준 설정이 필요합니다.
이를 위해서는 관측값 $y_i$와 추정된 직선에서의 ($b_0 + b_1x_i$)의 거리에 대한 정의가 필요합니다.
(1) 최소절대편차법 - Least Absolute Deviation method

(2) 최소제곱법 - Least Squares method
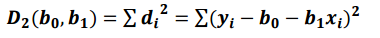
주로 최소제곱법을 이용하게 됩니다.
$b_0, b_1$에 대해 미분가능하여 거리를 최소로 만드는 $b_0, b_1$를 쉽게 찾을 수 있기 때문입니다.
4. 최소제곱법 - Least Squares method
최소제곱법으로 구한 $b_1$, $b_0$을 $\hat{\beta_1}$, $\hat{\beta_0}$ 으로 표현합니다.
최소제곱법은 $d_i$를 제곱한 값을 다 더한 것입니다.
이를 $b_0$, $b_1$로 미분하여 얻은 식을 연립방정식 계산을 하여 $\hat{\beta_1}, \hat{\beta_0}$를 구합니다.

5. 최소제곱추정값과 최소제곱추정량
최소제곱추정값은 실제 분석에 사용하고
최소제곱추정량은 통계적 추론(분포, 기댓값)할 때 사용합니다.
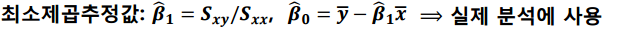

$\overline{y}$는 관측값, 상수이고 $\overlint{Y}$는 확률변수이기 때문입니다.
6. 적합값(Fitted value)와 잔차(residual)
(1) 적합값 - Fitted value
적합값은 적합하다고 추정, 예측한 값을 의미합니다.
적합회귀직선(추정회귀직선)은 다음과 같이 표시합니다.

적합값(예측값, predicted value)는 다음과 같습니다.

(2) 잔차 - residual
잔차는 관측값과 예측값과의 차이를 의미합니다.

최소제곱추정량을 유도하는 과정에서 두 가지 조건이 있습니다.
- 잔차의 합은 0

- x 곱하기 잔차의 합은 0
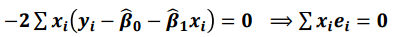
이 두 가지 조건 때문에 자유도는 m + n - 2가 됩니다.
7. 선형회귀모형에서의 모수 추정 예제

위 자료에서 연도에 따른 남성의 기록의 기울기와 절편을 추정하도록 하겠습니다.
우선 기울기와 절편을 구하기 위한 통계값을 구합니다.

이를 이용하여 최소제곱법으로 기울기와 절편을 추정합니다.
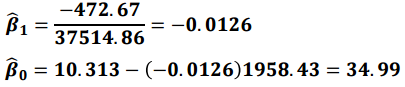
기울기와 절편으로 회귀직선을 구할 수 있습니다.
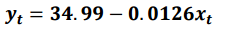
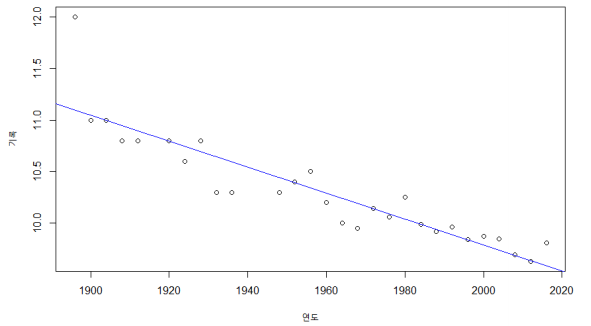
8. 단순선형회귀모형에서의 모수추정 정리

'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 회귀분석 - 회귀계수(기울기)에 대한 통계적 추론 - MSE, 구간추정, 가설검정, 검정통계량 (1) | 2020.10.18 |
|---|---|
| [통계학] 회귀추론을 위한 기본이론 - 회귀모델에서의 MSE와 중심축량 (1) | 2020.10.18 |
| [통계학] 회귀분석 - 회귀모형 개념 - 선형회귀모형 (0) | 2020.10.17 |
| [통계학] 다변량 자료 - 산점도와 상관분석 - 표준상관계수, 상관분석 예제 (0) | 2020.10.17 |
| [통계학] 이원배치 분산분석 - 반복이 있는 변량/혼합효과모형 (0) | 2020.10.14 |