여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
수치변수들 간의 관계를 간단히 알아보는 방법을 알아보겠습니다.
회귀 분석을 공부하기 전에 다변량 자료가 무엇인지 복습을 해보도록 하겠습니다.
다변량 자료 - Multivariate Data
다변량 자료는 어떤 대상에 대해 여러 가지 변수들을 관측(측정)한 자료들의 집함을 의미합니다
예) 신체검사 자료에서 연령, 성별, 신장, 체중 시력, 혈액형 등등

자료의 형태를 보면 변수가 여러개 인것을 확인할 수 있습니다.
이를 다변량 자료라고 합니다.
변수가 하나면 일변량 자료 입니다.
각각의 관측값 간에는 관력성이 없습니다.
이는 독립적인 관측값을 의미합니다.
다음에 배울 회귀 분석에서는 독립적인 관측값을 가정합니다.
다변량 자료에서의 주요 관심사
다변량 자료에서 주요 관심사는 변수들 간의 관계입니다.
1. 산점도와 상관분석으로 분석 가능한 관심사
(1) 변수들 간 관계가 있는가?
(2) 있다면 어떤 관계가 있는가?
(3) 관계가 어느 정도 되는가?
위 세 개의 관심사는 산점도와 상관분석을 통해 직선관계를 파악하여 분석할 수 있습니다.
산점도와 상관분석은 직선관계만 파악할 수 있습니다.
2. 회귀모형으로 분석 가능한 관심사
(1) 관계를 식으로 표시할 수 있는가?
(2) 관계식을 유도할 수 있는가?
(3) 유도된 관계식을 통해 다른 값을 예측할 수 있는가?
위 세 개의 관심사는 회귀분석으로 분석해야 합니다.
분석 목적이 관계유도 및 예측인 대표적인 모형이 회귀모형입니다.
산점도와 상관분석
변수들간의 직선 관계를 파악하는 산점도와 상관분석이 무엇인지 복습하겠습니다.

1. 산점도 - Scatter Plot
위 자료를 산점도로 표현하면 다음과 같습니다.

이처럼 데이터를 산점도로 나타내면 직선관계를 파악할 수 있습니다.
2. 상관분석 - Analysis of Correlation
상관분석은 상관계수를 구하여 모상관계수에 대한 추론과 검정을 하는 것입니다.
상관계수는 두 변수간의 직선(선형) 관계의 정도를 의미합니다.
공분산의 표준화된 값이 상관계수입니다.
표준상관계수는 다음과 같이 구할 수 있습니다.


표준상관계수가 0이면 직선관계가 없는것이고 1이나 -1에 근접한 값이면 직선 관계가 있다는 의미입니다.
따라서 가설검정을 할 때 귀무가설은 표본상관계수는 0이다로 설정합니다.
두 변수가 모두 정규분포를 따르면, $H_0$ : $rho$ = 0 에 대한 검정통계량은 다음과 같습니다.
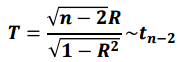
유의수준을 정하고 자유도가 n-2인 t분포의 임계값을 구한다면 신뢰구간을 추정할 수 있습니다.
이상점이 있는 경우 Spearman의 순위상관, Kendall의 tau 등 대체상관분석을 할 수 있습니다.
3. 상관분석 예제

위 자료에서 남자 자료만 이용하여 상관분석을 해보도록 하겠습니다.
우선 검정통계량과 상관계수를 구하기 위해 필요한 통계값을 구하겠습니다.
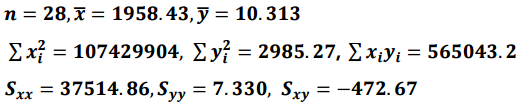
위 통계값을 이용하여 구한 상관계수는 다음과 같습니다.

검정통계량을 구하기 위한 통계값을 다 구했습니다.
검정통계량은 다음과 같습니다.

이를 0.01 유의수준에서 t분포의 임계값과 비교하겠습니다.

-2.47보다 작으므로 남자들의 자료는 직선 상관관계가 있음을 알 수 있습니다.
또한 표준상관계수가 -0.9이므로 -1에 가깝습니다.
이는 음의 기울기를 지닌다는것을 의미합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 단순선형회귀모형에서의 모수 추정 - 기울기와 절편, 최소제곱법, 최소절대편차법 (1) | 2020.10.17 |
|---|---|
| [통계학] 회귀분석 - 회귀모형 개념 - 선형회귀모형 (0) | 2020.10.17 |
| [통계학] 이원배치 분산분석 - 반복이 있는 변량/혼합효과모형 (0) | 2020.10.14 |
| [통계학] 이원배치 분산분석 - 반복이 있는 고정효과모형 - 상호작용 효과, 상호작용도표, 상호작용여부 (0) | 2020.10.14 |
| [통계학] 확률화 블록 계획법 - 이원배치 분산분석과의 차이점과 분석결과 해석 방법 (0) | 2020.10.14 |