여인권 교수님의 KMOOC 강의 "통계학의 이해 2"를 수강하면서 공부한 내용을 정리해보았습니다.
확률화블록설계의 개념과 단순 이원배치 분산분석과의 차이점을 알아보겠습니다.
확률화블록설계에 의한 분석결과를 어떻게 해석해야 하는지 알아보겠습니다.
확률화 블록 계획법
블록(block)은 요인의 처리 효과를 비교하는데 정확도를 높이기 위해 예비 지식을 이용하여 나눈 동일적인 실험 단위를 의미합니다.
예를 들어 수준(처리)는 처치 방법(관심 요인)이면 블록은 성별 또는 연령으로 구분할 수 있습니다.
쌍을 이룬 비교의 일반화(대응표본의 일반화)를 한 것입니다.
블록은 차이가 있다고 가정하므로 가설검정을 하지 않습니다.
1. 실험설계
p개의 수준(처리)과 b개의 블록이 있다고 가정하겠습니다.
각 블록 안에서 처리 배열은 확률적으로 결정하고 각 처리에 하나의 관측값을 배치합니다.
페니실린 생산량을 예시로 확인해보겠습니다.
페니실린 생산방식(A, B, C, D)에 따른 생산량을 비교하는 자료이며, 어떤 옥수수 담금액을 사용하는가에 따라 차이가 있다고 알려져 있습니다.
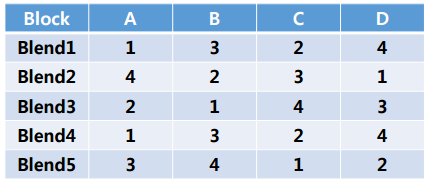
이처럼 수준과 블록을 표시할 수 있습니다.
이원배치와 유사한 자료형태이지만 블록효과는 유의성검정을 실시하지 않는 차이점이 있습니다.
2. 통계적 모형
모형식은 2요인 설계를 합니다.


3. 가설 검정
관심 요인의 처리효과 유무를 기준으로 귀무가설을 설정합니다.

주의할 점은 블록효과는 변동분해에서는 고려하지만 유의성검정을 실시하지 않습니다.
이 의미는 p-값이 커도 해당 변동을 오차변동에 포함시키지 않습니다.
4. 변동분해
변동분해를 통해 TSS, SSTR, SSBL, SSE를 구하고 검정통계량을 구할 수 있습니다.

5. 분산 분석표
변동분해한 값을 표로 정리한 것입니다.

블록의 처리효과가 없더라도 오차에 흡수시키지 않습니다.
블록효과의 F값이 1보다 클수록 블록화의 효과가 좋습니다.
6. 처리 평균 추정과 관심요인의 수준에 대한 다중비교
처리 평균의 구간추정은 다음과 같습니다.
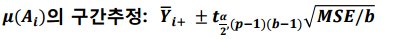
관심 요인의 수준에 대한 다중비교도 가능합니다.
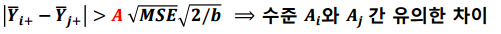
A에 이용되는 t분포 임계값은 어떤 방법을 이용하느냐에 따라서 달라집니다.
7. 예제
예제 문제를 풀어보겠습니다.
관심은 병아리의 체중이며
수준은 사료에 성장 촉진제(Control, Low dose, High dose)를 추가한 것입니다.
병아리의 크기가 유사한 것으로 블록을 한 자료입니다.

위 자료를 바탕으로 분산분석표를 만들면 다음과 같이 됩니다.
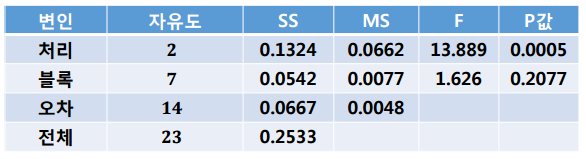
처리의 p값이 낮으므로 성장촉진제 양에 따라 병아리 성장에 차이가 있음을 알 수 있습니다.
다중비교는 다음과 같이 할 수 있습니다.
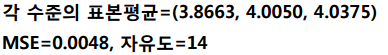

다중비교 방법을 정하고 MSE와 자유도를 대입하면 됩니다.
8. 정리

'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 이원배치 분산분석 - 반복이 있는 변량/혼합효과모형 (0) | 2020.10.14 |
|---|---|
| [통계학] 이원배치 분산분석 - 반복이 있는 고정효과모형 - 상호작용 효과, 상호작용도표, 상호작용여부 (0) | 2020.10.14 |
| [통계학] 변량효과모형과 혼합효과모형의 모형식과 통계적 추론 - 이원배치 분산분석 - 반복이 없는 경우 (0) | 2020.10.12 |
| [통계학] 고정효과모형의 모형식과 통계적 추론 - 이원배치 분산분석, 반복이 없는 경우 (0) | 2020.10.12 |
| [통계학] 분산분석 - 선형대비 - 수준 평균의 선형 결합 형태 (0) | 2020.10.10 |