여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
처리효과가 있다고 할 때, 수준 평균의 선형 결합 형태의 가설에 대한 검정 방법을 알아보겠습니다.
1. 선형대비 - Linear Contrast
선형대비는 고정효과모형에서만 이용할 수 있는 방법입니다.
선형대비는 계수의 합이 0인 $\mu_i$의 선형결합을 의미합니다.

$\mu_L$의 추정은 모평균을 표본평균으로 바꾸어 표현할 수 있습니다.

L은 정규분포를 따른다고 가정하면 분산과 분산의 추정량은 다음과 같습니다.
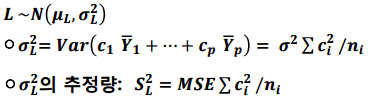
분산의 추정량을 구했으므로 중심축량을 도출할 수 있습니다.
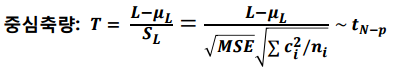
가설검정
선형대비에서 귀무가설을 다음과 같이 설정합니다.

중심축량에서 귀무가설을 대입하여 검정통계량을 도출합니다.

검정통계량은 자유도가 N-p인 t분포를 따르게 됩니다.
검정통계량을 제곱하면 F분포를 따르는 통계량을 구할 수 있습니다.
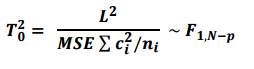
2. 예시 문제
단백질원료와 양에 따른 쥐의 체중증가 실험 자료입니다. 요인 1, 수준 4개 입니다.
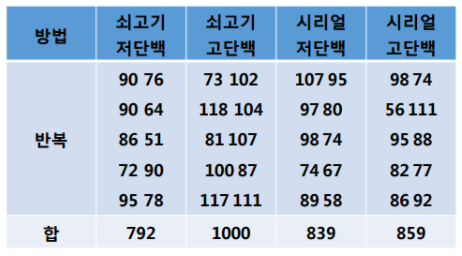
여기서 세 가지를 비교해보겠습니다.

(1) 단백질 원료(beef, cereal)에 따른 차이 비교

$t_0^2$값이 $F_{0.05,1,36}$보다 작으므로 단백질 원료에 따른 차이가 없다고 볼 수 있습니다.
(2) 단백질 양(Low, High)에 따른 차이비교

$t_0^2$값이 $F_{0.05,1,36}$보다 큽니다.
단백질 양에 따른 체중 증가량은 차이가 있다고 볼 수 있습니다.
(3) 사료 1은 A 제조사, 2, 3, 4는 B제조사 일 때, 제조사 간의 차이 비교

$t_0^2$값이 $F_{0.05,1,36}$ 보다 작으므로 차이가 없습니다.
여기서 사료 1에 계수는 3을 해줬습니다.
합만 0이 되면 됩니다
$s_L^2$에 반영이 되기 때문입니다.
그리고 (2)와 (3)에서 L은 비슷한 값을 보이고 있지만 검정결과는 다른 것을 확인할 수 있습니다.
3. 선형대비 정리

'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 변량효과모형과 혼합효과모형의 모형식과 통계적 추론 - 이원배치 분산분석 - 반복이 없는 경우 (0) | 2020.10.12 |
|---|---|
| [통계학] 고정효과모형의 모형식과 통계적 추론 - 이원배치 분산분석, 반복이 없는 경우 (0) | 2020.10.12 |
| [통계학] 분산분석 - 다중비교 - Fisher LSD, Bonferroni, Scheffe, Tukey HSD (0) | 2020.10.10 |
| [통계학] 분산분석 - 등분산성 검정 - 잔차그림, Hartley 검정, Bartlett 검정 (0) | 2020.10.10 |
| [통계학] 분산분석표, 고정효과모형과 변량효과모형에서 F통계량의 분모와 분자인 평균제곱의 통계적 성질 (0) | 2020.10.10 |