여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
회귀추론을 위한 기본이론
회귀모형의 모수 또는 예측값을 추론을 위한 기본 통계이론을 정리하겠습니다.
1. 회귀 모형식 가정
단순회귀모형에서 모형식은 다음과 같이 가정할 수 있습니다.

여기서, $\beta_0 + \beta_1x_i$는 평균을 의미합니다.
$\epsilon_i$ ~ iid N(0,$\sigma^2$)는 추론할 때 필요한 가정입니다.
최소제곱법에 의한 모수 추정에서는 특별히 오차항의 가정을 사용하지 않습니다.
최소제곱법은 $y_i - \beta_0 - \beta_1x_i$를 이용하기 때문에 $\epsilon_i$는 신경쓰지 않는다는 의미입니다.
모수 추정량 또는 예측값의 성질을 유도하기 위해 오차항의 가정이 필요합니다.
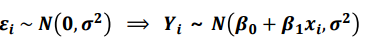
여기서 $\beta_0 + \beta_1x_i$ 는 평균을 의미하고 평균이 매번 바뀌므로 확률분포로 표현하기 위해 $u_i$로 표현합니다.
2. 표집분포
표집분포는 통계값의 확률분포를 의미합니다.
회귀모델에서 평균이 확률분포이므로 표본추출 값에 따라 평균이 바뀌기 때문입니다.

독립이므로 선형결합도 독립이고 분산은 각각의 분산의 합으로 표현할 수 있습니다.
이를 표준화하면 다음과 같게 됩니다.
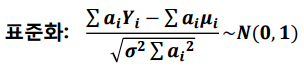
여기서 $\sigma^2$는 미지의 모수이므로 추정해야 합니다.
$\sigma^2$를 추정하는 방법은 모델마다 다릅니다.
회귀모형에서 분산을 추정하는 방법은 아래에 기술하겠습니다.

$\sigma^2$의 추정값은 $\hat{\sigma^2}$로 표현하며 이는 자유도가 v인 t분포를 따르게 됩니다.
3. $\sigma^2$의 추정 (복습)
$\sigma^2$를 추정하는 방법을 복습해보겠습니다.
(1) 단일 모집단의 경우 분산은 다음과 같이 추정할 수 있습니다.
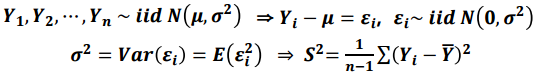
(2) 두 모집단의 평균이 다른 경우 분산은 다음과 같이 추정할 수 있습니다.

(3) 모집단이 세개 이상있을 때의 분산은 다음과 같이 추정할 수 있습니다.
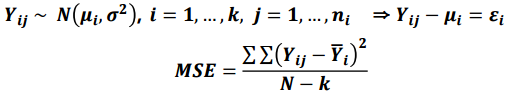
4. 회귀모형
회귀모형에서 분산은 추정하는 방법과 중심축량을 구하는 방법은 다음과 같습니다.
회귀모형식

MSE에서 분자는 (각각의 관측값 - 평균)제곱의 합으로 표현할 수 있습니다.
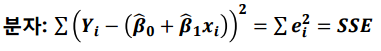
SSE / 자유도 = MSE 이므로 자유도를 알면 MSE를 구할 수 있습니다.
자유도는 오차의 두 제약조건 때문에 2개를 사용못합니다.

따라서 회귀모형에서 MSE(분산의 추정값)는 다음과 같이 구할 수 있습니다.

MSE(분산의 추정값)을 이용해서 중심축량을 구하면 다음과 같습니다.

중심축량 정규분포를 따르지 않고 자유도가 n-2인 t분포를 따르게 됩니다.
5. MSE 계산

6. 정리
회귀모형의 모수 또는 예측값을 추론하기 위한 기본 통계이론을 정리해보겠습니다.

'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 회귀분석 - 회귀계수(절편)에 대한 통계적 추론 - 절편의 중심축량과 구간추정 (0) | 2020.10.19 |
|---|---|
| [통계학] 회귀분석 - 회귀계수(기울기)에 대한 통계적 추론 - MSE, 구간추정, 가설검정, 검정통계량 (1) | 2020.10.18 |
| [통계학] 단순선형회귀모형에서의 모수 추정 - 기울기와 절편, 최소제곱법, 최소절대편차법 (1) | 2020.10.17 |
| [통계학] 회귀분석 - 회귀모형 개념 - 선형회귀모형 (0) | 2020.10.17 |
| [통계학] 다변량 자료 - 산점도와 상관분석 - 표준상관계수, 상관분석 예제 (0) | 2020.10.17 |