
Mathematics for Machine Learning 원서를 정리한 포스팅입니다. 공부 목적으로 중요하다고 생각하는 부분만 요약했습니다.
2.2 Matrices(행렬)
행렬은 연립 방정식을 간단히 표현하기 위해 사용됩니다. 또한 선형 함수(linear mapping)을 표현합니다.

(m, n)크기의 행렬입니다. m개의 행과 n개의 열로 이루어져 있습니다.
$R^{mxn}$ 공간에 있는 행렬의 열을 쌓으면 $R^{nm}$ 공간에 있는 긴 벡터로 표현할 수 있습니다.

2.2.1 Matrix Addition and Multiplication(행렬 덧셈과 곱셈)
(mxn) 동일한 크기의 두 행렬 A, B의 덧셈은 element-wise sum으로 정의됩니다.

행렬 곱셈은 element-wise operation으로 정의되지 않습니다. (mxn) 크기의 A행렬과 (nxk)크기의 B행렬을 곱한 C 행렬의 요소는 다음과 같이 구할 수 있습니다.

$c_{ij}$를 구하기 위해서 A행렬의 i번째 행과 B 행렬의 j번째 열을 곱하고 모두 더합니다. 그리고 행렬 곱셈은 A$\cdot$B로 표현합니다.
행렬 곱셈을 하기 위해서는 'neighboring' 차원이 같아야 합니다. 예를 들어 nxk 크기의 행렬 A는 kxm크기의 행렬 B과 곱해질 수 있습니다.

m과 n이 다르면 BA는 정의가 안됩니다. neighboring 차원이 일치하지 않기 때문입니다.
행렬 곱셈은 가환성을 만족하지 않습니다. AB != BA 입니다.
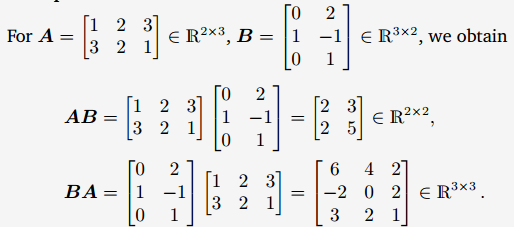
항등 행렬 정의
항등 행렬은 대각 요소가 1이고 나머지 요소가 모두 0인 행렬인 정사각행렬입니다.

행렬 곱셈의 성질
1. 연관 법칙
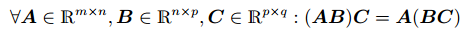
2. 분배 법칙

3. 항등 행렬과의 곱셈

2.2.2 Inverse and Transpose(역행렬과 전치행렬)
역행렬(Inverse)
nxn 크기의 A, B 행렬이 있습니다. AB = I = BA를 만족할 때, B 행렬은 A 행렬의 역행렬이라고 부르고 $A^{-1}$로 표기합니다. 만약 역행렬이 존재하면 행렬 A를 invertible이라고 부릅니다. 역행렬이 존재할 때, unique한 해를 갖습니다.
2x2 행렬의 역행렬을 계산하는 방법입니다.




전치행렬(Transpose)
A 행렬의 크기가 mxn, B행렬의 크기가 nxm 일때, $b_{ij}$ = $a_{ji}$를 성립하면 B를 A의 전치라고 표현합니다. 기호로는 $A^{\top}$ 으로 표시합니다. 일반적으로, $A^{\top}$는 A행렬의 열을 $A^{\top}$의 행으로 적을 때 얻어집니다.
전치행렬과 역행렬의 성질
다음은 역행렬과 전치행렬의 중요한 성질입니다.

대칭행렬(symmetric matrix)
행렬 A의 크기가 nxn 이고, $A = A^{\top}$이면, 행렬 A는 대칭행렬입니다. 대칭 행렬의 역행렬은 전치행렬과 같습니다. 두 대칭 행렬의 합은 항상 대칭 행렬입니다. 하지만, 곱셈은 항상 대칭행렬이 아닙니다.
2.2.4 연립 방정식의 간단한 표현
연립 방정식이 다음과 같이 주어졌을 때, 행렬 곱셈으로 표현할 수 있습니다.


'수학 > 기타 정리' 카테고리의 다른 글
| [통계학] 최대 우도 추정법(Maximum Likelihood) (0) | 2021.03.13 |
|---|---|
| [MML] ch 2.3 연립 방정식의 해(Solving Systems of Linear Equation) - 1 (0) | 2021.03.13 |
| [MML] 2.1 Systems of Linear Equations(연립 방정식) (0) | 2021.03.09 |
| [MML] ch 2. 선형 대수학(Linear Algebra) (0) | 2021.03.06 |
| [PRML] 1장 소개 (3) | 2021.01.15 |