최대 우도 추정에 대해서 공부하다가 이해가 잘 되도록 쉽게 설명해주는 유튜브가 있어서 내용을 정리해봤습니다!!
출처 : www.youtube.com/watch?v=XepXtl9YKwc
예를 들어, 쥐들의 무게를 잰다고 가정해보겠습니다.

최대 우도의 목적은 데이터 분포를 맞추기 위한 최적의 방법을 찾는 것입니다.
다양한 데이터 타입에 대한 다양한 분포가 존재합니다. 정규분포, 지수분포, 감마분포 등등 여러 분포가 존재합니다. 데이터 분포를 맞추려고 하는 이유는 작업하기가 쉽고 더 일반적이기 때문입니다. 이 경우에 몸무게가 정규 분포를 따른다고 생각할 수 있습니다. 정규분포는 많은 것들을 의미합니다.

첫 번째로 대부분의 쥐 몸무게는 평균에 가깝습니다.
두 번째로 쥐 몸무게가 평균을 중심으로 대칭입니다. 관측값이 완벽하게 대칭은 아니지만 한쪽으로 심각하게 치우치지 않습니다.
정규 분포는 다양한 형태가 존재합니다.

정규분포의 형태가 Skinny일 수도 있고 Medium 이나 Large Boned 일 수도 있습니다.
형태를 정하고나면 중심을 어디에 둘지 찾아야 합니다. 정규분포를 하나 정해서 데이터가 정규분포를 따르는지 보겠습니다.
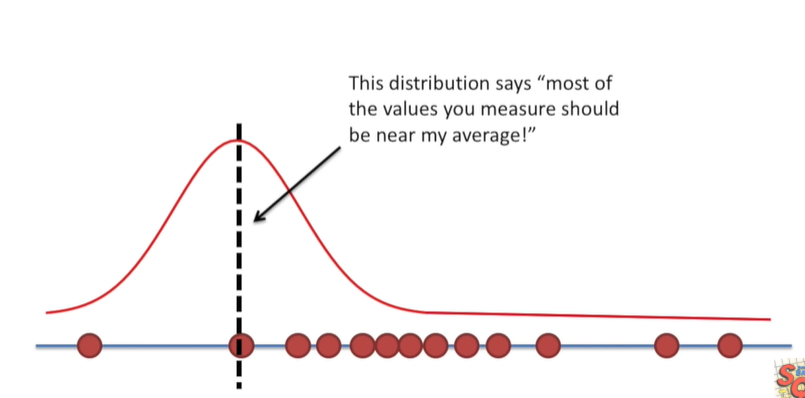
분포의 평균은 검은 점선입니다. 이 경우는 실제 관측치(쥐몸무게)와 평균이 다릅니다. 관측치가 대부분 평균과 떨어져 있습니다. 이 경우에 멀리 떨어져 있는 관측치의 모든 확률 또는 우도가 낮습니다.
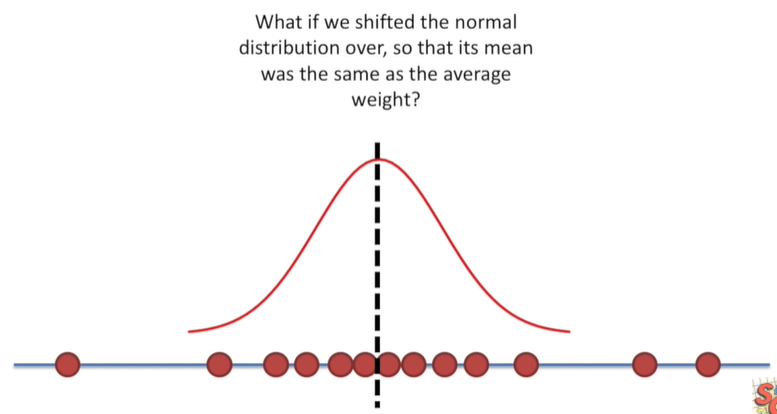
정규분포의 위치를 움직이면 어떨까요? 분포의 평균이 몸무게의 평균과 같도록 이동시킵니다. 이 경우에 몸무게의 확률 또는 우도가 비교적 높아집니다. 정규분포를 계속해서 오른쪽으로 움직이면 평균과 멀리 떨어져 있는 관측치의 확률 또는 우도가 낮아집니다.
분포의 중심 위치를 기준으로 데이터의 우도를 표시할 수 있습니다.

왼쪽부터 시작해서 데이터의 우도를 오른쪽으로 이동시키면서 우도를 계산합니다. 가능한 모든 위치에서 우도를 계산한 뒤에 측정된 관측치의 우도를 최대화할 수 있는 위치를 찾습니다. 찾은 분포의 평균의 위치는 관측한 몸무게의 우도를 최대합니다. 이 위치가 최대 우도 추정법으로 찾은 평균입니다.
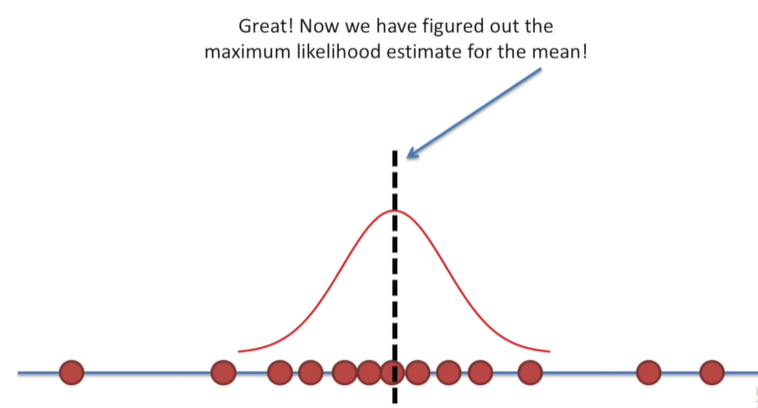
분포의 평균 이외에도 표준편차를 기준으로 데이터의 최대 우도를 표시할 수 있습니다.

측정한 몸무게의 우도를 최대로하는 표준 편차를 찾습니다. 이처럼 관측치에 대한 우도를 최대화하는 평균 또는 표준편차를 찾을 수 있습니다.
일반적으로 확률과 우도는 같은 말입니다. 통계학 관점에서 우도는 관측치에 대한 평균 또는 표준편차의 최적 값을 찾는 상황에서 관련하여 사용하는 용어입니다. 이것이 데이터를 어떤 분포에 부합하는지 찾는법입니다.
'수학 > 기타 정리' 카테고리의 다른 글
| [MML] Ch 2.4 벡터 공간(Vector Spaces) (0) | 2021.03.18 |
|---|---|
| [MML] ch 2.3 연립 방정식의 해(Solving Systems of Linear Equation) -2 (0) | 2021.03.17 |
| [MML] ch 2.3 연립 방정식의 해(Solving Systems of Linear Equation) - 1 (0) | 2021.03.13 |
| [MML] ch 2.2 행렬(Matrices) (0) | 2021.03.12 |
| [MML] 2.1 Systems of Linear Equations(연립 방정식) (0) | 2021.03.09 |