
Mathematics for Machine Learning를 공부하고 정리한 포스팅입니다.
2.3.2 기본 행 연산(Elementary Transformations)
연립 방정식을 풀기위한 핵심은 기본 행 연산(elementary transformation)입니다. 기본 행 연산은 정답을 변화시키지 않고 연립방정식을 간단한 형태로 변환합니다.
기본 행 연산에는 세 가지가 있습니다.
(1) 두 행을 교환하기(행렬에서 행은 방정식을 나타냅니다.
(2) 행에 상수를 곱하기
(3) 서로 다른 두 행을 더하기
행렬에 기본 행 연산을 거쳐서 행 사다리꼴(row-echelon form)으로 바꾸면 특이해와 일반해를 쉽게 구할 수 있습니다. 다음 예제를 통해 살펴보겠습니다.
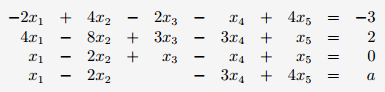
위 연립 방정식을 첨가행렬(augmented matrix)로 나타냅니다. 그리고 첫 번째 행과 세 번째 행을 교환합니다.

첫 번째 행의 첫 번째 요소 아래를 다 0으로 만듭니다.

위 과정을 반복하면 아래와같은 행-사다리꼴이 완성됩니다.

각 행의 첫번째 요소를 pivot이라고 합니다. pivot이 존재하는 열을 pivot column이라고 합니다. pivot column에 해당하는 x는 basic variable, non-pivot column에 해당하는 x는 free variable이라고 부릅니다. 이제 특이해를 구해보겠습다. 특이해는 Ax=b를 만족하는 x입니다. free variable에 0을 대입하면 쉽게 구할 수 있습니다.

free variable인 x2와 x4에 0을 대입하여 x1, x3, x4를 구합니다. 이것이 특이해 입니다.
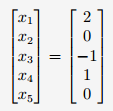
이제 일반해를 구해야 합니다. Ax=0을 만족하는 x를 구한다음에 특이해와 더하면 일반해를 구할 수 있습니다. Ax=0을 만족하는 x는 non-pivot column을 pivot column으로 표현하는 x를 찾으면 됩니다.

2.3.3 The Minus-1 Trick
The Minus-1 Trick은 제차 연립 방정식(homogeneous system of linear equations) Ax=0을 찾기 위한 방법입니다.
아래와 같은 행렬이 주어졌을 때, Minus-1 Trick을 이용하여 Ax=0 해를 찾겠습니다.

위 행렬은 기본 행 연산으로 만들어진 reduced row echelon form 입니다. 행을 추가하여 nxn 크기로 만듭니다. 그리고 non-pivot column에 -1을 추가합니다.

이제 -1을 포함하는 열이 Ax=0의 해가 됩니다.

A행렬의 pivot column은 Ax=b의 해 공간의 기저(basis)를 형성합니다. A 행렬의 -1 pivot column은 Ax=0 해공간의 기저를 형성합니다. 그리고 이것을 kernel 또는 null space라고 부릅니다.
Calculating the Inverse
Ax = I를 만족하는 x가 $A^{-1}$입니다. Ax=I를 풀기 위해 첨가 행렬(augmented matrix)로 나타낼 수 있습니다.

이제 이 A를 I로 만들어주면, 첨가 행렬의 right-hand side가 $A^{-1}$이 됩니다. 결국, 역행렬을 구하는 것은 연립방정식을 푸는 것과 동일합니다.
다음과 같이 주어진 행렬의 역행렬을 구하겠습니다.

Ax=I를 첨가행렬로 나타냅니다.

행연산을 통해 A를 I로 만듭니다.
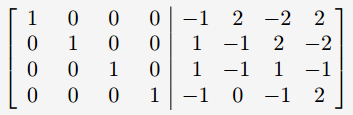
첨가 행렬의 right-hand side가 A의 역행렬입니다.

2.3.4 Algorithms for solving a System of Linear Equation
지금까지 Ax=b를 푸는 방법에 대해서 간단히 알아보았습니다. Ax=b에 해가 없는 경우는 어떻게 구할 수 있을까요? 9장에서 배울 선형 회기(linear regression)을 사용하여 근사화로 풀 수 있습니다.
어떤 경우에 Ax=b를 풀기 위해 A의 역행렬을 구해야 합니다. x = $A^{-1}$b를 구하면 x를 구할 수 있기 때문입니다. 이 경우는 A가 square matrix이고 invertible한 조건이 있어야 합니다. 다른 방법은 A가 선형 독립 열들을 갖고 있을 때, transpose를 이용하면 Ax=b를 근사화 할 수 있습니다. $A^{T}A$는 대칭 행렬이 됩니다. 따라서 invertible합니다. 이 성질을 이용하여 다음과 같이 x를 근사화 할 수 있습니다. 이 방법을 Moore-Penrose pseudo-inverse 라고 합니다. 이 방법으로 Ax=b를 풀면 x는 least-squares solution에 해당합니다.
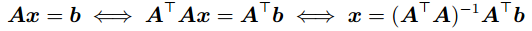
이 방법의 단점은 $A^{T}A$를 계산하는 과정에서 많은 연산량이 필요합니다. Ax=b를 푸는 다른 방법을 살펴보겠습니다.
가우시안 소거법은 행렬식(determinant) 계산하기, 벡터 집합이 선형 독립인지 확인하기, 행렬의 rank 계산하기, 벡터 공간의 기저 계산하기 등 다양하게 이용됩니다. 가우시안 소거법은 연립방정식을 푸는 직관적이고 간단한 방법입니다. 하지만 행렬의 크기가 커지면 엄청나게 많은 연산량이 필요합니다.
다음 방법은 반복 방법(iterative methods) 입니다.
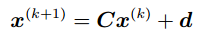
매 반복마다 C와 d가 잔여 오차(residual error)인 ll$x^{k+1} - x_{*}$ll를 감소시킵니다. 결국 x로 수렴합니다.
'수학 > 기타 정리' 카테고리의 다른 글
| [MML] Ch 2.4 벡터 공간(Vector Spaces) (0) | 2021.03.18 |
|---|---|
| [통계학] 최대 우도 추정법(Maximum Likelihood) (0) | 2021.03.13 |
| [MML] ch 2.3 연립 방정식의 해(Solving Systems of Linear Equation) - 1 (0) | 2021.03.13 |
| [MML] ch 2.2 행렬(Matrices) (0) | 2021.03.12 |
| [MML] 2.1 Systems of Linear Equations(연립 방정식) (0) | 2021.03.09 |