최대 마진 분류기(The Maximal Margin Classifier)
데이터를 초평면을 사용하여 완벽하게 분류할 수 있다면 무한개의 초평면이 존재할 것입니다. 초평면이 어느 관측치와도 만나지 않으면서 약간 위 아래로 움직일 수 있기 때문입니다. 분리 초평면을 사용한 분류기를 구성하기 위하여 어떤 초평면을 사용해야 할지 합리적인 방법이 있어야 합니다.

training observation으로부터 가장 멀리 떨어진 분리 초평면(separating hyperplane)인 최대 마진 초평면(maximal margin hyperplane)을 선택하는 것이 자연스럽습니다. 즉, 주어진 분리 초평면 부터 각 training observation 까지의 수직 거리를 계산하고 가장 작은 거리를 마진(margin)이라고 부릅니다.
최대 마진 초평면(maximal margin hyperplane)은 마진(margin)이 가장 큰 분리 초평면 입니다. 즉, 초평면과 training observation 사이의 수직 거리의 최소값이 가장 큰 경우를 의미합니다. 최대 마진 초평면에 기반하여 test observation를 분류할 수 있습니다. 이를 최대 마진 분류기(maximal margin classifier)이라고 합니다.
최대 마진 분류기는 잘 작동하지만 p가 큰 경우에 과적합을 초래할 수 있습니다.
p차원에서 최대 마진 분류기는 다음과 같이 정의할 수 있습니다.
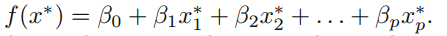
이 값의 부호에 따라 x의 class를 할당합니다. 위 그림은 관측값과 초평면 사이의 최소 거리가 최대가 되도록 계산된 초평면 입니다. 이 maximal margin hyperplane은 두 클래스 사이에 끼울 수 있는 가장 넓은 평판을 나타낸다고 생각할 수 있습니다.
위 그림에서 3개의 observation이 maximal margin hyperplane과 거리가 동일하여 margin의 넓이를 타나내는 점선을 따라 놓여져 있습니다. 이 세개의 observation은 서포트 벡터(support vector)라고 부릅니다. 왜냐하면 이들은 p차원 공간에서 벡터이고 만약 이 점들이 조금 움직이면 최대 마진 초평면 또한 움직이기 때문에 최대 마진 초평면을 support 하기 때문입니다.
이 최대 마진 초평면은 다른 observation이 아닌 support vector에 의존합니다. 어떤 observation의 움직임이 마진에의해 설정된 경계를 넘어가지 않는다면 분리 초평면과 margin에 영향을 미치지 않습니다.
최대 마진 초평면(maximal margin hyperplane)이 observation의 작은 부분 집합에만 의존한다는 중요한 성질은 추후에 공부할 support vector classifier와 support vector machine을 다룰 때 살펴보겠습니다.
최대 마진 분류기 제작하기
n개의 training observation에 기반한 최대 마진 초평면을 구축하는 방법을 살펴보겠습니다. 요약하자면 최대 마진 초평면은 최적화 문제에대한 해답입니다.
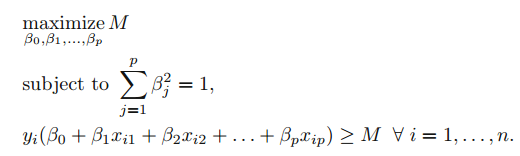
M은 margin을 의미합니다. 최대 마진 분류기의 계수 $\beta$에 대한 제약조건이 주어진 상태에서 M을 최대화 하는 최적화 문제를 푸는 것입니다. 각 제약조건을 하나하나 살펴보겠습니다.

위 제약 조건은 M이 양수이면 각 관측치가 초펴연의 올바른 쪽에 있게 되도록 보장합니다. 관측치가 M 만큼의 거리를 가지고 초평면과 떨어져 있습니다.

이 제약 조건은 i번째 관측치에서 초평면 까지의 수직 거리는 다음에 의해 주어진 다는 것을 보여줍니다.
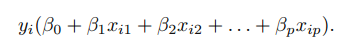
즉, M은 초평면의 margin을 나타내고 M을 최대화하는 $\beta$를 선택하는 최적화 문제입니다.
분류 불가능한 경우
만약 분리 초평면이 존재하는 경우에 최대 마진 분류기는 분류를 수행하기 위한 자연스러운 방법입니다. 하지만 많은 경우에 분리 초평면이 존재하지 않고 또한 최대 마진 분류기도 수행하지 못합니다. 즉, 아래 그림처럼 training observation이 두 개의 class로 분할되지 않는 경우를 의미합니다.

이처럼 분류 할수 없는 경우에 대한 최대 마진 분류기의 일반화는 서포트 벡터 분류기(support vector classfier)이라고 알려져 있는데 다음 포스팅에서 공부해보도록 하겠습니다. 이처럼 분류할 수 없는 경우에 soft margin를 사용하여 클래스들을 거의 분류하는 초평면을 개발하 수 있습니다.
참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 비선형 결정 경계(Non-linear Decision Boundaries) (0) | 2021.08.03 |
|---|---|
| [ISLR] 서포트 벡터 분류기(Support Vector Classifiers) (0) | 2021.08.02 |
| [ISLR] 부스팅(Boosting) (0) | 2021.07.31 |
| [ISLR] 랜덤 포레스트(Random Forests) (0) | 2021.07.31 |
| [ISLR] 배깅(Bagging) (0) | 2021.07.31 |