K-평균 군집화(K-Means Clustering)
K-means clustering은 데이터 셋을 K개의 구별되고 겹치치 않는 cluster으로 분할하는 방법입니다. k-means clustering을 수행하기 위하여 cluster의 수 K를 정해야 합니다. 그리고나서 K-means algorithm은 각 관측값을 정확히 K개의 cluster 중 하나에 할당합니다. 아래 그림은 150개의 관측치로 구성된 데이터에 서로 다른 K값을 사용하여 K-means clustering을 수행한 결과입니다.

K-means Clustering 절차
$C_1, ... C_K$를 각 cluster 내 관측치들의 인덱스들을 포함하는 집합이라고 하겠습니다. 이 집합은 두 가지 성질을 갖습니다.
1. 각 관측치는 적어도 K개 cluster중 하나에 속합니다.
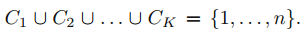
2. cluster는 겹치지 않습니다. 즉, 한개를 초과하여 cluster에 할당된 관측치는 없습니다.
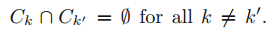
cluster 내 변동이 가능한 적어야 좋은 clustering 이라고 합니다. cluster $C_k$의 클러스너 내 변동(within-cluster variation) W($C_k$)는 cluster 내 관측치들이 서로 얼마나 다른지에 대한 정도입니다. 따라서 within-cluster variation W($C_k$)을 최소화하는 문제를 풉니다.
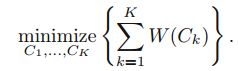
이는 모든 K개 cluster에 대해 합한 total within-cluster variation을 가능한 최소가 되도록 모든 관측값들을 K개의 cluster로 분할한다는 것을 의미합니다.
위 문제를 푸는 것은 적합해 보이지만 within-cluster variation을 정의해야 합니다.

k번째 cluster의 within-cluster variation는 k번째 cluster 내 관측치 사이의 모든 쌍 유클리디안 거리 제곱의 합입니다. 그리고 k 번째 cluster내에 속하는 관측치들의 수로 나눕니다. 즉, k-means clustering은 아래의 최적화 문제를 풉니다.
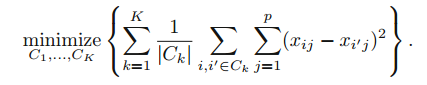
위 식을 해석하면 동일 cluster 내 존재하는 관측치들의 거리가 최소화 하는 것입니다. 위 식을 풀기 위한 알고리즘을 찾아야 합니다. 즉, 위 식을 최소화하여 관측값들을 K개 cluster로 분할하는 방법을 찾아야 합니다.
n개의 관측값들을 K개 cluster로 분할하는 방법은 $K^n$개의 방법이 존재합니다. 이를 K와 n이 큰 경우에 이를 푸는 것은 불가능 합니다. 다행히 국소 최적값(local optimum)을 제공하는 간단한 방법이 있습니다. K-means optimization 입니다.

1. 각 관측치에 1에서 K까지의 숫자를 랜덤하게 할당합니다. 이는 관측치들에 대한 초기 클러스터 할당입니다.
2. 클러스터 할당이 변하지 않을 때까지 다음을 반복합니다.
(a) 각 K개 클러스터에 대해 클러스터 중심을 계산합니다. k번째 클러스터 중심은 k번째 클러스터 내 관측치들에 대한 p 변수 평균들의 벡터입니다.
(b) 각 관측치를 무게중심이 가장 가까운 클러스터에 할당합니다.

K-means algorithms은 전역 최적값(global optimum)이 아니라 국소 최적(local optimum)을 제공하므로 결과는 초기 클러스터링 할당에 의존합니다. 이러한 이유로 여러 무작위 초기값으로 알고리즘을 여러번 수행하는 것이 중요합니다. 그리고나서 가장 좋은 결과(목적 함수가 제일 낮은 값)를 선택합니다.
아래 그림은 서로 다른 초기값에 대하여 k-means clustering을 수행한 결과입니다.

참고자료 및 그림 출처
Gareth James의 An Introduction to Statistical Learning
'수학 > Statistical Learning' 카테고리의 다른 글
| [ISLR] 주성분 분석(PCA, Principal Components Analysis) (0) | 2021.08.05 |
|---|---|
| [ISLR] 서포트 벡터 머신(SVM, Support Vector Machine) (0) | 2021.08.03 |
| [ISLR] 비선형 결정 경계(Non-linear Decision Boundaries) (0) | 2021.08.03 |
| [ISLR] 서포트 벡터 분류기(Support Vector Classifiers) (0) | 2021.08.02 |
| [ISLR] 최대 마진 분류기(The Maximal Margin Classifier) (0) | 2021.08.02 |