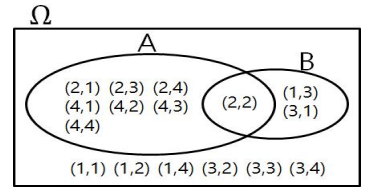
고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다. 이번 포스팅에서는 표본 공간(Sample space)와 사건(Event), 실험(Experiment) 용어를 살펴보도록 하겠습니다. 표본 공간과 사건(Sample Space and Events) 표본 공간(Sample Space): 실험으로 나온 모든 결과를 담고 있는 집합입니다. 실험(Experiment): 데이터 집합을 생성하는 과정입니다. 사건(Event): 표본 공간의 부분집합 입니다. 표본 공간에는 두 종류가 있습니다. 이산형 표본 공간(Distcrete Sample Space): 이산형 데이터를 담고 있는..