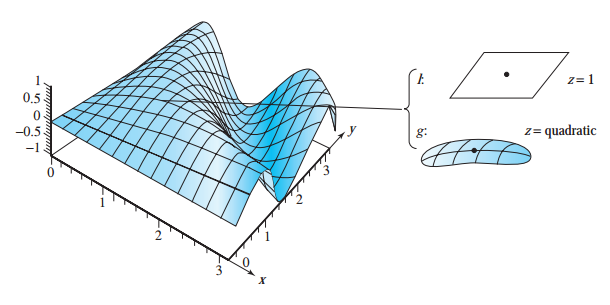
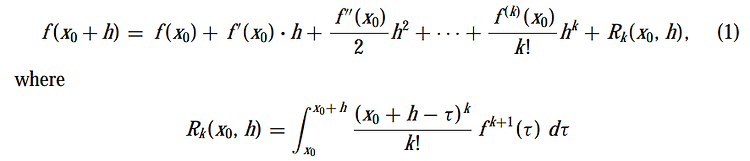이전 포스팅에서는 일변수함수에 대한 테일러 정리를 살펴보았습니다. 이번에는 다변수함수에 대한 테일러 정리를 공부하겠습니다. 다변수함수에 대한 테일러 정리(Taylor's Theorem for Many Variables) 만약 n개의 변수를 취하는 실함수(real valued function with n variables) f가 x0에서 정의된다면 다음과 같이 정의할 수 있습니다. 그리고나서, 미분가능성의 정의에의해 나머지항 R1(x0,h)는 점 x0에서 1차에서 사라집니다. 그러므로 일차 테일러 공식(First-Order Taylor Formula)는 다음을 얻습니다. xi는 n개의 다변수에 해당하는 변수입니다. 각 개별적인 다변수에대해 hi가 존재합니다. 이차 테일러 공식은 다음과 같습니다. 이차 테일..