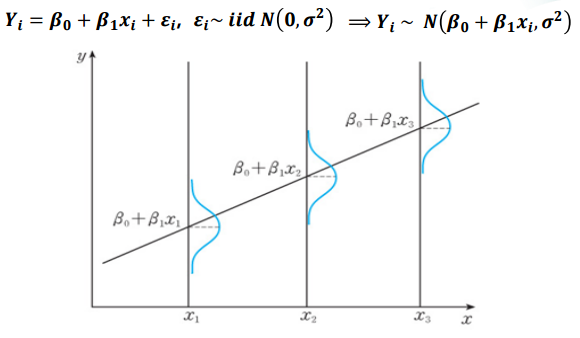
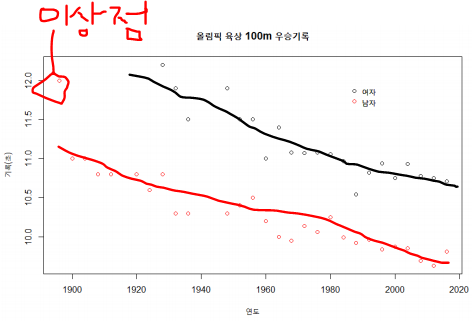
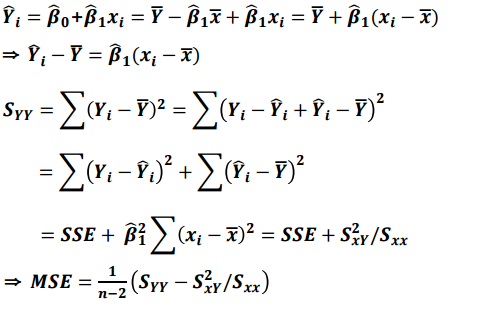여인권 교수님의 KMOOC 강의 를 수강하면서 공부한 내용을 정리해보았습니다. 회귀추론을 위한 기본이론 회귀모형의 모수 또는 예측값을 추론을 위한 기본 통계이론을 정리하겠습니다. 1. 회귀 모형식 가정 단순회귀모형에서 모형식은 다음과 같이 가정할 수 있습니다. 여기서, $\beta_0 + \beta_1x_i$는 평균을 의미합니다. $\epsilon_i$ ~ iid N(0,$\sigma^2$)는 추론할 때 필요한 가정입니다. 최소제곱법에 의한 모수 추정에서는 특별히 오차항의 가정을 사용하지 않습니다. 최소제곱법은 $y_i - \beta_0 - \beta_1x_i$를 이용하기 때문에 $\epsilon_i$는 신경쓰지 않는다는 의미입니다. 모수 추정량 또는 예측값의 성질을 유도하기 위해 오차항의 가정이 필요합..