여인권 교수님의 KMOOC 강의 <통계학의 이해 2>를 수강하면서 공부한 내용을 정리해보았습니다.
예측값 평균에 대한 통계적 추론
예측값의 평균, E(Y) = $b_0$ + $b_1x$를 추론하기 위한 중심축량과 예측구간을 알아보겠습니다.
1. 반응변수 기댓값 E($Y_k$)에 대한 추론
주의할 점은 $Y_k$를 직접 추론하는 것이 아니라 E($Y_k$)를 추론하는 것입니다.

점추정량의 성질에 대해 알아보겠습니다.
점추정량을 Y들의 선형 결합으로 나타낼 수 있습니다.
이는 정규분포를 따른다는 것을 의미합니다.
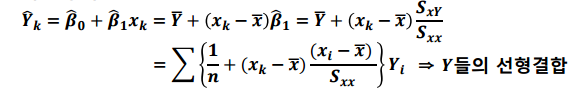
추정된 예측값 평균은 다음과 같이 표시할 수 있습니다.
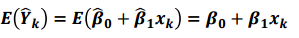
분산은 다음과 같습니다.
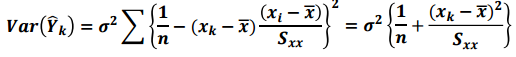
이는 $x_k$가 $\overline{x}$에서 멀어질수록 분산이 커진다는 것을 의미합니다.
평균과 분산을 구했으므로 $\hat{Y_k}$를 정규분포로 나타낼 수 있습니다.
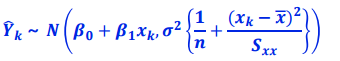
이를 정규화하면 중심축량을 구할 수 있습니다.
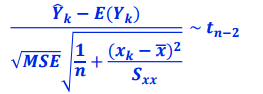
중심축량을 통해 100(1-a)% 예측구간을 구할 수 있습니다.
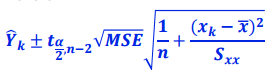
2. 예제 문제
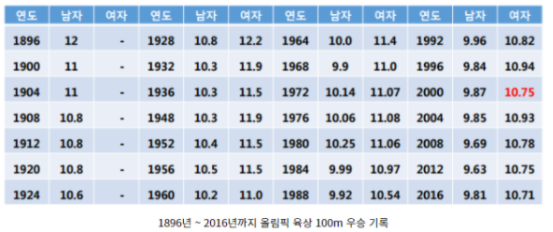
올림픽 육상 100m 우승 기록에서 남자의 자료에 대해 예측값 평균에 대해 통계적 추론을 해보겠습니다.
우선 회귀모델을 설계하고 기울기와 절편을 추론합니다.
기울기와 절편을 추론하는 방법은 이전 포스팅에 알아보았습니다.
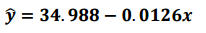
위 회귀모델을 이용하여 2024년 우승 기록 평균 예측 값을 구해보겠습니다.
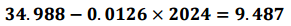
2024년 우승기록 평균의 예측구간은 다음과 같이 구할 수 있습니다.
우선 n, $\overling{x}$, $S_{xx}$, MSE 를 구해야 합니다.
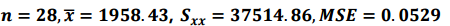
이를 통해 예측구간을 구할 수 있습니다.

3. 정리
예측값의 평균에 대한 중심축량과 예측구간에 대해 알아보았습니다.
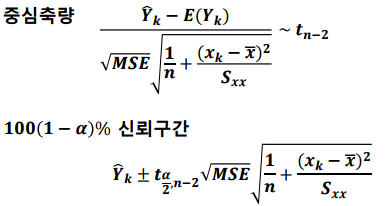
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 회귀분석 - 새로운 관측값에 대한 예측 - 중심축량과 예측구간 (0) | 2020.10.19 |
|---|---|
| [통계학] 회귀분석 - 회귀계수(절편)에 대한 통계적 추론 - 절편의 중심축량과 구간추정 (0) | 2020.10.19 |
| [통계학] 회귀분석 - 회귀계수(기울기)에 대한 통계적 추론 - MSE, 구간추정, 가설검정, 검정통계량 (1) | 2020.10.18 |
| [통계학] 회귀추론을 위한 기본이론 - 회귀모델에서의 MSE와 중심축량 (1) | 2020.10.18 |
| [통계학] 단순선형회귀모형에서의 모수 추정 - 기울기와 절편, 최소제곱법, 최소절대편차법 (1) | 2020.10.17 |