(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다.
상대도수의 극한의 개념으로 이해하는 확률에 대해 알아보겠습니다.
이를 통해 확률이 모집단에 대한 것임을 이해해보겠습니다.
2.2 상대도수의 극한개념
(1) 통계적 확률(statistical probability)
통계적 확률이란 각각의 실험에서 발생하는 결과는 표본이고 실험을 무한히 반복한다는 것은 표본이 결국 모집단이 된다는 의미입니다. 결국, 확률은 모집단이 어떤 형태로 구성되어 있는지를 보여주게 됩니다.
동전의 앞면이 나올 사건을 A라고 하면 P(A) = 1/2입니다. 이는 앞면과 뒷면의 발생가능성이 동일하다고 가정하는 고전적 확률입니다. 동전 던지기 실험결과를 통해 확률에 대한 상대도수의 극한(통계적 확률)을 보여드리겠습니다.
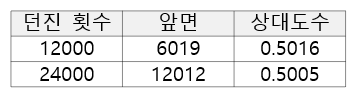
이 표에서 실험횟수가 어느 정도 큰 경우 상대도수가 0.5 근처에 있는 것을 볼 수 있습니다. 이는 상대도수가 0.5에 수렴한다는 것을 의미합니다. 동전을 던진 횟수에서 앞면이 나온 횟수의 비율을 구하여 확률을 근사값으로 사용하자는 것입니다.

만약 실험을 무한히 반복한다면 n(A)/n은 어떤 값으로 수렴하는데 이 극한 값을 사건 A가 일어날 확률로 해석하자는 것 입니다. P(A)는 동일한 확률실험을 n번 반복할 때 실험에서 사건 A가 발생한 비율의 극한값으로 수식으로 표시하면 다음과 같습니다.

실험을 계속 반복한다는 것은 표본을 계속 뽑는다는 것을 의미하며 실험을 무한 반복하면 표본이 무한히 많아져 결국 모집단이 될 것입니다. 즉, 확률은 표본이 아니라 모집단이 어떤 형태로 이루어져 있는지는 표시한 것입니다. 상대도수의 극한은 많은 표본을 통해 모집단의 특성을 파악한다고 해서 통계적확률이라고 합니다.
몬테카를로 적분
몬테카를로 적분은 무한히 실험을 반복하는 통계적 확률을 이용한 적분입니다.
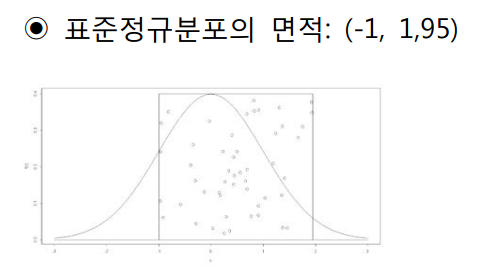
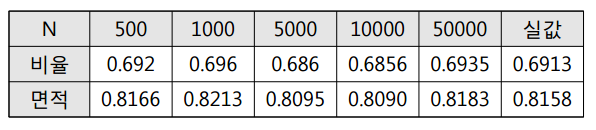
표준정규분포의 (-1, 1.95) 구간의 면적을 구하려 할때 함수가 어려워 적분으로 구하기 어렵습니다. 만약 몬테카르토 적분을 이용한다면 쉽게 구할 수 있습니다. 사각형 범위에 있는 난수를 생성해 난수가 표준정규분포에 포함되는지 안되는지 비율을 확인합니다. 이 비율을 사각형 면적에 곱한다면 (-1, 1.95) 구간의 면적을 구할 수 있습니다.
이상으로 상대도수의 극한의 개념으로 이해하는 확률(통계적 확률)을 알아보았습니다. 이를 통해 확률이 모집단에 대한 것임을 이해하였습니다. 추가적으로 몬테카를로 적분을 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 06-1. 조건부 확률 (1) - 조건부 확률의 정의와 응용사례 (0) | 2020.09.16 |
|---|---|
| [통계학] 05. 확률의 기본 정리 - 확률의 공리, 기본 성질 (0) | 2020.09.15 |
| [통계학] 04-3. 확률(3) - 경우의 수 (조합, 중복조합, 순열, 중복순열) (0) | 2020.09.15 |
| [통계학] 04-2. 확률(2) - 확률의 이해 (고전적 확률, 연속표본공간) (0) | 2020.09.15 |
| [통계학] 04-1. 확률 (1) - 기본개념 (확률, 확률실험, 표본공간, 사건, 집합의 연산법칙, 벤다이어그램) (0) | 2020.09.15 |