(통계학-기본개념과 원리, 여인권)을 바탕으로 제작하였습니다.
(k-mooc 통계학의 이해1, 여인권)을 수강하면서 공부한 내용을 정리해보았습니다.
확률의 공리와 이를 기반으로 유도된 확률에 대한 기본 성질을 알아보겠습니다.
2.3 공리적 확률
공리란 증명할 수 없으나 옳다고 판단되는 명제입니다. 확률이론들은 확률의 공리를 토대로 만들어졌습니다. 표본공간상에서 아래의 공리를 만족하는 P()를 확률측도(probability measure)라고 하고 P(A)를 사건 A의 확률이라고 합니다.
확률의 공리에 대해서 알아보겠습니다.
확률의 공리
공리 1. P(Ω) = 1
공리 2. 사건 A $\subset$ Ω에 대해, 0 $\leq$ P(A) $\leq$ 1
공리 3. 서로배반인 사건 A와 B에 대해, P(AUB) = P(A) + P(B)
공리 1은 어떤 실험의 결과는 표본공간 Ω에서 항상 일어남을 뜻합니다.
공리 2는 어느 사건도 확률이 음수가 될 수 없고 1보다 클 수도 없음을 뜻합니다.
공리 3은 서로배반인 두 사건 A와 B에 대해 합사건의 확률은 각각의 확률의 합과 같음을 의미합니다.
3. 확률의 기본정리
확률의 공리로부터 얻을 수 있는 확률의 기본적인 성질을 알아보겠습니다. 먼저 성질에 대해 정리하고 설명을 하겠습니다.
확률의 기본 성질
1. P($A^c$) = 1 - P(A)
2. A $\subset$ 이면 P(A) $\leq$ P(B)
3. P(AUB) = P(A) + P(B) - P(A$\cap$B)
4. P(AUB) $\leq$ P(A) + P(B)
몇 가지 중요한 성질을 살펴보도록 하겠습니다.
첫 번째 성질
P($A^c$) = 1 - P($A$) 또는 P($A$) = 1 - P($A^c$) 입니다. 이것은 Ω = $A$ U $A^c$이며 $A$와 $A^c$는 상호배반이므로 공리 1과 공리 3에 의해
1 = P(Ω) = P($A$U$A^c$) = P($A$) + P($A^c$)
가 되어 P($A^c$) = 1 - P($A$) 또는 P($A$) = 1 - P($A^c$)가 성립합니다. 이 성질을 이용하면 P($\pie$) = 0 인 것을 쉽게 보일 수 있습니다.
문제를 풀어보겠습니다. 즉석복권을 1000장 발행했는데 이 중 4장이 당첨복권입니다. 어떤 사람이 4장의 복권을 구입할 때 적어도 한 장 이상의 당첨복권을 구입하게 될 확률을 구해보겠습니다. 이 때 첫 번째 성질을 이용하면 쉽게 구할 수 있습니다. 한 장 이상의 당첨복권을 구입할 사건을 $A$라고 하면 $A^c$는 구입한 4장 모두 당첨되지 않을 사건으로 경우의 수 계산이 훨씬 간단합니다. 그러므로 1에서 $A^c$의 확률을 뺸 값으로 $A$의 확률을 계산하는 것이 더 효율적입니다.

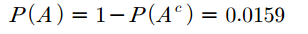
확률의 기본 성질
5. $P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)$
6. n개의 사건 $A_1, A_2, ... , A_n에 대해

이 식은 5번 성질을 여러 개의 변수로 확대한 것입니다.
7. 부울의 부등식

부울의 부등식을 이용하면 합사건에 대한 확률의 경계값을 유도할 수 있습니다. $A_i$를 $A_i^c$로 대체하면 본페르니 부등식을 유도할 수 있습니다.
8. 본페로니 부등식

본페로니 부등식을 이용하면 교사건에 대한 확률의 경계값을 구할 수 있습니다. 이 식은 분사분석에서 이용됩니다.
이상으로 확률의 공리와 기본 성질을 알아보았습니다. 감사합니다.
'수학 > 기초 통계학' 카테고리의 다른 글
| [통계학] 06-2. 조건부 확률 (2) - 독립사건 (0) | 2020.09.16 |
|---|---|
| [통계학] 06-1. 조건부 확률 (1) - 조건부 확률의 정의와 응용사례 (0) | 2020.09.16 |
| [통계학] 04-4. 확률(4) - 통계적 확률 (상대도수의 극한개념, 통계적확률, 몬테카를로 적분) (0) | 2020.09.15 |
| [통계학] 04-3. 확률(3) - 경우의 수 (조합, 중복조합, 순열, 중복순열) (0) | 2020.09.15 |
| [통계학] 04-2. 확률(2) - 확률의 이해 (고전적 확률, 연속표본공간) (0) | 2020.09.15 |