반응형
고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

기하 분포(Geometric Random Variable)
독립적인 베르누이 시행을 첫 번째로 성공할 때까지 시행하는 것입니다.
확률 변수 X는 첫 번째로 성공할 때까지 시행한 횟수 입니다.
확률 함수는 다음과 같이 정의됩니다.

n-1번 실패하고 n번째 성공할 확률 입니다.
예를 들어, 5번 시행때 첫 성공이 발생했다면 확률질량함수는 다음과 같이 정의할 수 있습니다.
P{X=5} = $(1-p)^4p$
기하 분포는 파라미터 p를 지닌 기하 확률질량함수로부터 발생된 확률들의 분포입니다.
그리고 기하확률질량함수의 모든 합은 1입니다.

기하 분포의 기대값과 분산
기하 분포의 파라미터는 p(성공확률) 입니다.
기대값과 분산은 파라미터의 함수이고, 다음과 같이 정의됩니다.

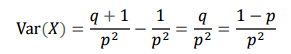
기하 분포 예시 문제
항아리에 N개 흰공, M개 검은공이 들어있습니다. 검은 색공이 뽑힐 때까지 공을 임의로 뽑습니다. 각 공이 복원추출일 때 다음 확률은 어떻게 될까요?
우선 확률 변수를 정의합니다.
X : 검은색 공이 첫 번째 뽑힐때까지 필요한 횟수
P(흰공) = N/(N+M)
P(검은공) = M/(N+M)
1) n번째에 검은색 공이 뽑힐 확률
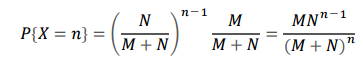
2) 적어도 k 번째에서 검은 공을 뽑을 확률
k-1번까지 흰공이 뽑힌 확률을 계산하면 됩니다.

반응형
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 이산형 확률분포 - 초기하 분포 (1) | 2021.02.14 |
|---|---|
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |
| [확률론] 이산형 확률분포 - 포아송 분포 (0) | 2021.02.10 |
| [확률론] 이산형 확률분포 - 이항분포 (0) | 2021.02.08 |
| [확률론] 이산형 확률분포 - 베르누이 분포 (3) | 2021.02.07 |