고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

포아송 분포(Poisson distribution)
확률 변수 X가 이산형 값인 0,1,2,... 중 하나를 취할 때 파라미터 $\lambda$를 지닌 포아송 확률 변수라고 정의합니다.
$\lambda$(람다) = np는 단위 시간 동안 특정 사건이 몇번 발생한 것인지를 나타냅니다. 단위 시간동안 사건의 평균 발생 회수로 이해하면 됩니다.
그리고 포아송 확률 변수에서 나온 실수를 확률로 변환해주는 확률질량함수는 다음과 같이 정의됩니다.
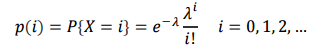
포아송 확률질량함수는 실수를 확률로 대응하는 함수이므로 모든 값을 더하면 1이 됩니다. 실제로 테일러급수 전개를 해보면 합이 1이 되는 것을 확인할 수 있습니다.

포아송 확률질량함수로 나오는 확률들의 패턴을 포아송확률분포 라고 합니다.
그러면 포아송 분포는 언제 이용할까요??
포아송 분포는 단위 시간안에 특정 사건이 몇번 발생할 것인지를 표현하는 확률 분포입니다.
포스팅 아래에 예제 문제를 풀어보면서 어떤 문제에 포아송 분포를 이용하는지 알아보겠습니다.
포아송 분포의 모수(파라미터)인 람다($\lambda$)
모수는 분포의 모양을 결정하는 중요한 값입니다.
포아송 분포도 모수인 람다에 따라 분포의 모양이 달라집니다.

포아송 분포와 이항 분포의 관계
이항 분포의 파라미터는 n과 p입니다.
n이 충분히 크고 p가 작을 때, 이항 분포는 포아송 분포로 근사화할수 있습니다.
아래는 수학적인 증명입니다.

즉, 성공확률이 p인 독립 시행을 np가 적당한 값을 갖도록 n이 크고 p가 작도록 n번을 수행하면, 발생한 성공 회수는 파라미터 람다 $\lambda$ = np를 지닌 포아송 확률 변수입니다.
포아송 분포는 단위 시간동안 특정 사건이 얼마나 발생했는지에 대한 확률을 구할 때 이용합니다.
사건이 드물게 발생했을 때, 포아송 분포 모델이 잘 들어맞습니다.
포아송 확률 변수의 몇 가지 예제를 살펴보겠습니다.
(1) 마을에서 100세 이상 사람들의 수
(2) 페이지에서 오타의 수
(3) 하루에 전화를 잘못걸 확률
포아송 분포의 기대값과 분산
포아송 분포의 기대값과 분산은 둘 다 $\lambda$ = np로 동일합니다.
기대값 E[X] = $\lambda$
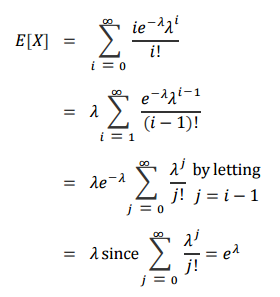
분산 V[X] = $\lambda$


포아송 분포 예시 문제
문제 1
책 한 페이지에서 오타 수는 $\lambda$ = 0.5를 지닌 포아송 분포를 따른다고 가정하겠습니다. 한 페이지에서 오타가 적어도 1개 이상 발생할 확률을 구하는 문제입니다.
우선 확률 변수를 정의합니다.
X = 오타의 수 = {0, 1, 2, 3, ... }
오타가 적어도 1개 이상 발생할 확률은 오타가 발생하지 않는 확률의 여사건으로 구할 수 있습니다.

'수학 > 확률론' 카테고리의 다른 글
| [확률론] 이산형 확률분포 - 음이항 분포 (0) | 2021.02.13 |
|---|---|
| [확률론] 이산형 확률분포 - 기하분포 (2) | 2021.02.12 |
| [확률론] 이산형 확률분포 - 이항분포 (0) | 2021.02.08 |
| [확률론] 이산형 확률분포 - 베르누이 분포 (3) | 2021.02.07 |
| [확률론] 분산과 표준편차 (2) | 2021.02.06 |