고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

이항 분포(Binomial Distribution)
베르누이 실험을 한 번 한것을 베르누이 시행이라고 합니다.
이항 분포는 독립적인 베르누이 시행을 n번 한것 입니다.
독립적인 베르누이 시행이므로 첫 번째 시행은 두 번째 시행에 영향을 주지 않습니다.
확률 변수 X는 n번 시행에서 성공횟수로 정의합니다.
이항 분포의 확률질량함수(pmf)는 다음과 같습니다.

이항 분포는 이항확률함수로부터 나온 확률들의 패턴을 말합니다. 그리고 모수(parameter) n과 p를 갖고 있습니다.
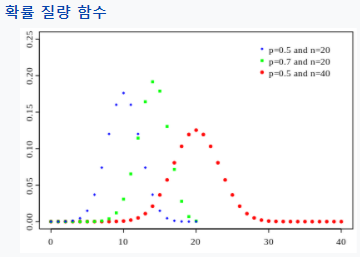
그림을 보면 모수인 p와 n에 따라 분포의 모양이 다르다는 것을 확인할 수 있습니다.
이처럼 모수는 확률분포 모양을 결정하는 수입니다.
모든 확률함수에는 하나 이상의 파라미터가 있습니다.
이항분포는 n,p
베르누이분포는 p (n이 항상 1입니다)
이항 분포의 기대값과 분산
기대값과 분산은 모수로 정의되는 값입니다.
이항 분포의 기대값과 분산을 살펴보겠습니다.
확률 변수 X를 모수 n과 p를 지닌 이항확률변수로 정의하겠습니다.
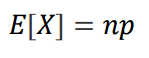

베르누이 분포의 기대값은 p, 분산은 p(1-p) 였습니다.
이항 분포는 n개의 독립적인 베르누이 분포의 합으로 생각해볼 수 있습니다.
따라서 기대값은 np, 분산은 np(1-p)로 이해할 수 있습니다.
예시 문제
제품이 불량일 확률 0.01, 정상일 확률은 0.99입니다. 하나의 박스에 10개의 제품이 포함되어 있습니다. 박스에 2개 이상 불량품이 발견되면 환불을 해줍니다. 회사가 환불을 해야하는 확률은 어떻게 될까요?
10개 제품에서 2개이상이 불량품일 확률을 구하면 됩니다.
우선 확률 변수를 정의합니다.
X : 결함의 수, X={0,1,...,10}
그리고 모수 n=10, p=0.01입니다.
2개 이상이 불량품일 확률은 다음과 같이 구할 수 있습니다.

그리고 기대값과 분산은 다음과 같습니다.
E[X] = 10 * 0.01 = 0.1
V[X] = 10 * 0.01 * 0.99 = 0.099
이항 분포의 성질
모수 n, p를 지닌 이항 확률 변수 X가 있고, k는 0부터 n까지의 임의의 수라고 가정하겠습니다.
P{X=k}는 처음에는 단조 증가하고 k가 (n+1)p 이상의 값을 갖게 되면 단조 감소합니다.
증명
어떤 k부터 P(X=k)/P(X=k-1)이 1보다 큰지 작은지 구함으로써 증명할 수 있습니다.
1보다 크면 P(X=k)값이 크다는 의미이고, 1보다 작으면 P(X=k-1)값이 크다는 의미입니다.


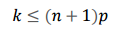
K가 (n+1)p값 이하일 때는 P(X=k)/P(X=k-1)이 1이상이 되어 분포가 증가하는 형태를 뜁니다.
K가 (n+1)p 초과하면 분포는 감소하는 형태를 뜁니다.
그림으로 살펴보겠습니다.


k <= (n+1)*p <= 5.5
k가 5이하의 값일 때는 분포는 증가하고 5이후 감소합니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 이산형 확률분포 - 기하분포 (2) | 2021.02.12 |
|---|---|
| [확률론] 이산형 확률분포 - 포아송 분포 (0) | 2021.02.10 |
| [확률론] 이산형 확률분포 - 베르누이 분포 (3) | 2021.02.07 |
| [확률론] 분산과 표준편차 (2) | 2021.02.06 |
| [확률론] 기댓값(Expectation) (1) | 2021.02.05 |