고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

기대값(Expected Value)
확률론에서 가장 중요한 개념중 하나는 확률 변수의 기대값입니다.
만약, X가 확률질량함수(pmf) p(x)를 지닌 이산 확률 변수이면, X의 기대값은 E[X]로 표현하고 다음과 같이 정의됩니다.
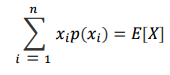
산술 평균과 기대값의 차이점은 p(x)에 있습니다. 산술 평균은 p(x)가 다 동일하고, 기대값은 가중 평균을 이용합니다. 각각의 X에 가중치인 p(x)를 적용하는 것입니다.
예시 문제 1
게임에서 이길 확률은 0.99 입니다. 만약 이기면 100원을 받고, 지면 100,000원을 잃습니다. 확률 변수 X는 게임에서 얻는 돈의 양으로 정의하겠습니다. X의 기대값 E[X]는 무엇일 까요?
E[X] = 100 * 0.99 - 100,000 * 0.01 = -901 입니다.
한 게임당 얻는 돈의 기대값은 -901원이 되어, 게임을 무수히 많이 진행하게 되면 결과적으로 돈을 잃게 됩니다.
예시 문제 2
이산형 확률 변수 예제입니다. 동전을 두 개 던졌을 때, 확률 변수 X를 앞면의 수로 정의하겠습니다. X가 가질 수 있는 값은 X = {0, 1, 2} 가 됩니다. X의 기대값 E[X]는 무엇일 까요?
각각의 확률을 먼저 구합니다.
p(0) = 1/4, p(1) = 1/2, p(2) = 1/4
E[X] = 0 * 1/4 + 1 * 1/2 + 2 * 1/4 = 1 이 됩니다.
예시 문제 3
앞면이 나올 확률이 p인 동전을 독립적으로 두 번 던졌습니다. 확률 변수 X를 앞면이 나온 숫자로 정의할 때, 기대값 E[X]는 무엇일 까요?
확률 변수 X가 가질 수 있는 갑은 X = {0, 1, 2} 입니다.
성공 확률 = p, 실패 확률 = 1-p 입니다.
각각의 확률 변수의 확률을 구해보겠습니다.
P(0) = (1-p)(1-p)
P(1) = p(1-p)
P(2) = pp
E[X] = 0 * (1-p)(1-p) + 1 * p(1-p) + 2 * pp = 2p 가 됩니다.
확률 변수의 함수의 기대값(Expectation of a function of a Random Variable)
확률 변수의 기대값 E[X]가 아니라 확률 변수의 함수 g(X)에 대한 기대값을 구하는 방법입니다.
pmf p(x)를 지닌 이산형 확률 변수 X에 대해, X의 함수 g(X)의 기대값은 다음과 같음과 같이 구할 수 있습니다.

이는 곧 g(x)의 가중 평균으로 생각해 볼 수 있습니다.
p(x)가 가중치가 되는 것입니다.
예시 문제를 풀어보면서 이해해보도록 하겠습니다.
예시 문제 1
두 개의 동전을 던졌을 때, 확률 변수 X를 앞면의 수로 정의하겠습니다.
그리고 X의 함수 g(x)를 3/(X+1)로 정의하겠습니다. 이때, g(x)의 기대값은 어떻게 될까요?
X가 가질 수 있는 값은 X={0, 1, 2}가 됩니다.
우선 각각의 확률을 정의해줍니다.
p(0) = 1/4, p(1) = 1/2, p(2) = 1/4
E[g(x)] = (3/(0+1)) * 1/4 + (3/(1+1)) * 1/2 + (3/(2+1)) * 1/4 = 7/4 가 됩니다.
기대값의 성질(Properties of Expectation)
기대값은 세 가지 성질을 갖습니다.
(1) 상수 c의 기대값은 상수가 됩니다.
E[c] = c
(2) E[cX] = cE[X]가 됩니다.
안쪽에 있는 상수 c를 바깥쪽으로 꺼낼 수 있습니다.
(3) E[cX + d]에서 c와 d가 상수일 때, E[cX + d] = cE[X] + d가 됩니다.
(1), (2) 성질을 결합한 것입니다s.
확률 변수 X의 n차 적률(nth moment of a random variable X)
기대값 E[X]는 X의 1차 적률 또는 평균이라고 부릅니다.
E[$X^2$]는 X의 2차 적률 또는 분산이라고 부릅니다.
E[$X^n$]은 확률 변수 X의 n차 적률이라고 부릅니다. 그리고 다음과 같이 구할 수 있습니다.

확률 변수 X가 주어졌을 때, 그 X의 n승의 기대값을 n차 적률(n th moment)라고 부르는 것입니다.
적률에 대해서는 추후에 적률 생성 함수에서 자세히 다뤄보도록 하겠습니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 이산형 확률분포 - 베르누이 분포 (3) | 2021.02.07 |
|---|---|
| [확률론] 분산과 표준편차 (2) | 2021.02.06 |
| [확률론] 확률변수와 확률함수 (1) | 2021.02.01 |
| [확률론] 독립 사건 (0) | 2021.01.31 |
| [확률론] Odds(오즈, 아즈) (0) | 2021.01.29 |