고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

확률변수(Random Variable)
확률 변수는 확률과 통계에서 매우 중요한 개념입니다. 어떤 의미를 갖고 있는지 알아보도록 하겠습니다.
확률 변수는 표본 공간에 있는 모든 원소를 실수로 대응하는 함수입니다.
여기서, 표본 공간에 존재하는 모든 원소는 실험에서 나온 결과입니다.
그림으로 한번 살펴보겠습니다.

즉, 표본 공간에 있는 원소가 확률 변수라는 함수를 만나면 실수로 바뀌게 됩니다.
실수 = f(표본 공간의 원소)
이해를 돕기 위해 몇 가지 예시를 살펴보겠습니다.
예시 문제 1
3개의 동전을 던졌습니다. 동전은 앞면 또는 뒷면만 결과로 나옵니다.
표본 공간 = {(HHH), (HHT), (HTH), (THH), (HTT), (THT), (TTH), (TTT)}
표본 공간에 총 8개의 원소가 존재합니다.
그리고 확률 변수(Y)를 앞면이 나온 갯수로 정의하겠습니다.
표본 공간의 원소가 확률 변수를 거치게 되면 0,1,2,3 실수로 바뀌게 됩니다.
Y = {0, 1, 2, 3}

이처럼 data를 분석하려면 우선 실수로 바꿔야 합니다.
확률변수의 두 가지 종류
확률변수는 두 가지 종류가 존재합니다.
(1) 이산형 확률변수(Discrete random variables)
확률변수 결과값이 유한개의 이산형(셀 수 있는) 값입니다.(0, 1, 2, 3, ...)
ex) 3개의 동전을 던졌을 때 앞면의 개수, 한달에 닭이 낳는 알의 개수 등등
(2) 연속형 확률변수(Continuous random variables)
확률변수 결과값이 무한개의 연속형(셀 수 없는) 값입니다.
ex) 전구의 수명, 서울 시민의 연소득
확률함수(Probability Function)
표본공간에 존재하는 모든 원소가 확률변수에 의해 실수로 변환되었습니다.
이 실수를 확률로 바꿔주는 함수가 확률함수입니다.
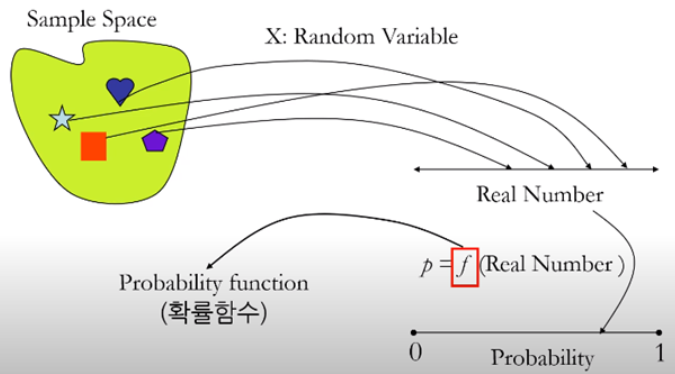
확률함수에는 두 가지 종류가 있습니다.
확률함수의 종류
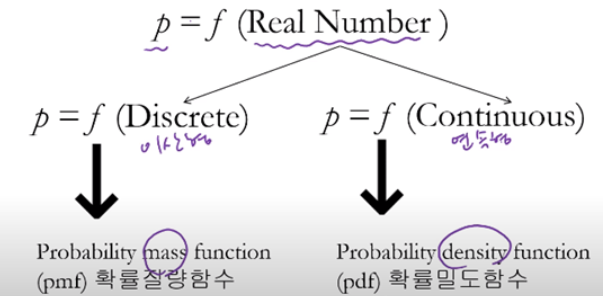
(1) 확률 질량 함수(pmf, Probability Mass Function)
확률변수 X가 이산형일 때, 이 값들을 확률로 대응하는 함수(P[X=x])입니다.

pmf는 확률의 특성을 다 갖고 있습니다.
(a) 0 <= p(x) <= 1 for all x
(b) 모든 p(x)의 합은 1
(2) 확률 밀도 함수(pdf, Probability density function)
확률변수 X가 연속형일 때, 이 값들을 확률로 대응하는 함수입니다.
pdf에 대해서는 다음에 살펴보도록 하겠습니다.
확률 질량 함수(pmf) 예시 문제
동전을 두 개 던졌습니다.
표본 공간 = {(HH), (HT), (TH), (TT)}
확률 변수 X : 앞면의 개수 = {0, 1, 2}
확률 변수 X를 확률 질량 함수로 나타내면 다음과 같습니다.
P(X=0) = 1/4
P(X=1) = 2/4
P(X=2) = 1/4
확률 질량 함수 결과값을 이용하여 확률 분포로 나타내면 다음과 같습니다.

그리고 각 확률은 0과 1사이에 있고, 모든 확률의 합은 1이므로 pmf의 성질을 만족합니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 분산과 표준편차 (2) | 2021.02.06 |
|---|---|
| [확률론] 기댓값(Expectation) (1) | 2021.02.05 |
| [확률론] 독립 사건 (0) | 2021.01.31 |
| [확률론] Odds(오즈, 아즈) (0) | 2021.01.29 |
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |