고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.
김성범 교수님의 확률 강의는 정말 명강의라고 생각합니다! 확률론에 관심있으신 분은 유튜브 강의를 시청해보시는 것을 추천드리겠습니다.

베이즈 룰(Bayes' Rule)
베이즈 룰은 이전 포스팅에서 공부했던 조건부 확률을 응용한 문제입니다.
베이즈 룰이 무엇인지 알아보도록 하겠습니다.
$A_1, A_2, A_3$을 표본 공간 S의 부분 집합이고, 이들은 상호 배타라고 해보겠습니다.
그리고 사건 B가 다음과 같다고 가정하겠습니다.
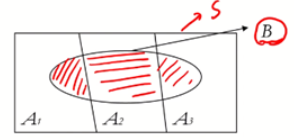
표본 공간 S를 3개의 상호 배타적 집합으로 나눈 것입니다. 이때 사건 B에 관심이 있을 때 B의 확률은 어떻게 구할 수 있을 까요??

이처럼 관심있는 특정 사건의 확률은 조건부확률의 합으로 표현할 수 있습니다.
이것이 베이즈 정리의 시작이 됩니다.
그리고 이를 전확률 법칙(Law of Total Probability)라고 합니다.
P($A_1$), P($A_2$), P($A_3$)와 P(B l $A_1$), P(B l $A_2$), P(B l $A_3$)를 알고 있으면
P($A_1$ l B), P($A_2$ l B), P($A_3$ l B)를 구할 수 있습니다.
베이즈 정리를 이용하는 이유는 확률 P(B l $A_n$)은 구하기 쉽기 때문에 이를 활용하여 P($A_n$ l B)를 구하는 것입니다.

이처럼 알고 있는 조건으로 확률을 구하는 것이 베이지룰입니다.
그리고 이 각각의 확률들의 명칭을 정의할 수 있습니다.
(1) 사전 확률(Prior probability)
P($A_1$), P($A_2$), P($A_3$)
(2) 사전정보 조건부확률(Data probability)
P(B l $A_1$), P(B l $A_2$), P(B l $A_3$)
(3) 사후 확률(Posterior probability)
P($A_1$ l B), P($A_2$ l B), P($A_3$ l B)
그리고 사후 확률이 구하고 싶은 확률이 됩니다.
김성범 교수님은 사후 확률을 정보 B가 주어졌을 때 $A_1$의 확률이므로 $A_1$이 정보 B에 의해 update가 되었다고 설명해 주셨습니다. 이 설명을 듣고 조건부확률이 어떤 의미를 갖고 있는지 이해할 수 있게 되었습니다. 정말 명강의라고 생각합니다. 확률론에 관심있으신 분은 김성범 교수님의 유튜브 강의를 시청하는 것을 추천드립니다.
정보를 받기 전 P($A_1$)은 사전 확률이고 정보를 받은 후 갱신된 $A_1$의 확률은 P($A_1$ l B) 사후 확률이 됩니다.
이처럼 사후확률은 사전확률의 업데이트 버전으로 생각해볼 수 있습니다.
몇 가지 예시 문제를 통해 베이즈 정리의 이해도를 높여보도록 하겠습니다.
예시 문제 1
회사는 공급처 1과 2에서 타이어를 구매합니다. 공급처 1의 타이어에는 10%의 결함이 발생하고, 공급처 2의 타이어에는 5%의 결함이 발생합니다. 그리고 공급처 1에서 전체 타이어의 40%를 구매합니다. 타이어에 결함이 발생했을 때, 이 결함이 공급처 1의 타이어일 확률은 어떻게 될까요?

우선 각 이벤트를 정의해보겠습니다.
(1) 사전 확률
P(S1) = 0.4
P(S2) = 0.6
(2) 사전정보 조건부확률
P(D l S1) = 0.1
P(D l S2) = 0.05
이제 관심있는 확률은 P(S1 l D) 입니다.
이는 다음과 같이 구할 수 있습니다.
P(S1 l D) = P(S1 D) / P(D)
= (P(D l S1) * P(S1)) / P(D)
= (P(D l S1) * P(S1)) / (P(S1)P(D l S1) * P(S2)P(D l S2))
= (0.4 * 0.1) / (0.4 * 0.1 + 0.6 * 0.05)
= 0.57
예시 문제 2
사업 수완을 배우는 A, B 두 가지 방법이 있습니다. A가 실패할 확률은 20%, B가 실패할 확률은 10% 입니다. 하지만 B가 더 비싸서 B는 30%만 이용을 합니다. 노동자가 사업 수완을 배웠는데, 실패를 했습니다. 노동자가 방법 A로 학습을 받았을 확률은 어떻게 될까요??
우선 각 사건을 정의해줍니다.
(1) 사전 확률
P(A) = 0.7
P(B) = 0.3
(2) 사전정보 조건부확률
P(F l A) = 0.2
P(F l B) = 0.1
(3) 사후 확률(관심있는 확률이자 문제에서 묻는 확률)
P(A l F) = P(AF) / P(F)
P(AF)는 교집합이므로 조건부 확률로 나타낼 수 있습니다.
P(F)는 전확률법칙에 의해서 확장할 수 있습니다.
따라서 다음과 같이 됩니다.
P(A l F) = (P(A) * P(F l A)) / (P(A) * P(F l A) + P(B) * P(F l B))
예시 문제 3
범죄 조사에서 용의자가 범죄를 저질렀을 확률은 0.6 입니다. 하지만 범죄자가 갖고 있을 특성(왼손잡이 등)이 발견되었습니다. 이러한 특성을 일반 사람이 갖고 있을 확률은 0.2 입니다. 용의자가 이러한 특성을 갖고 있을 때, 범죄를 저질렀을 확률은 어떻게 될까요??
각 사건을 정의해 봅시다.
(1) 사전 확률
P(G) = 0.6
P(~G) = 0.4
(2) 사전정보 조건부확률
P(C l G) = 1 (범죄자가 갖고 있는 특성은 100% 입니다.)
P(C l ~G) = 0.2
(3) 사후 확률(관심있는 사건 또는 문제에서 묻는 확률)
P(G l C) = P(GC) / P(C) = (P(G) * P(C l G)) / (P(G) * P(C l G) + P(~G) * P(C l ~G))
예시 문제 4
전체 인구 중 1%가 특정 질병에 고통을 받고 있습니다. 혈액 검사를 했을 때, 질병을 가진 사람이 양성이 나올 확률은 97%이고 건강한 사람이 질병을 갖고 있다고 판단할 확률은 6% 입니다.
우선 각 사건을 정의하겠습니다.
(1) 사전 확률
P(D) = 0.01
P(~D) = 0.99
(2) 사전 정보 조건부 확률
P(+ l D) = 0.97
P(- l D) = 0.03
P(+ l ~D) = 0.06
P(-ㅣ~D) = 0.94
문제에서는 세 가지 확률을 묻고 있습니다.
(a) 양성 반응이 나올 확률 P(+)
P(+) 는 전확률 법칙으로 구할 수 있습니다.
P(+) = P(D) * P(+ l D) + P(~D) * P(+ l ~D)
(b) 양성이 나왔는데 실제로 질병을 갖고 있을 확률 P(D l +)
P(D l +) = (P(D) * P(+ l D)) / (P(D) * P(+ l D) + P(~D) * P(+ l ~D))
(c) 음성이 나왔는데 실제로 건강할 확률 P(~D l -)
P(~D l -) = P(~D) * P(- l ~D) / (P(D) * P(- l D) + P(~D) * P(- l ~D))
'수학 > 확률론' 카테고리의 다른 글
| [확률론] 독립 사건 (0) | 2021.01.31 |
|---|---|
| [확률론] Odds(오즈, 아즈) (0) | 2021.01.29 |
| [확률론] 조건부 확률과 확률의 곱셈 법칙 (1) | 2021.01.28 |
| [확률론] 확률의 공리와 기본 성질(Axioms and Basic Properties of Probability) (4) | 2021.01.25 |
| [확률론] 집합 연산(Set Operation)과 집합 연산의 법칙(Laws of Set Operation) (1) | 2021.01.25 |