고려대학교 김성범 교수님의 확률/통계 강의와 교재 'Sheldon Ross, A First Course in Probability (10th edition)' 를 공부하고 정리한 내용입니다.

조건부 확률(Conditional Probability)
조건부 확률은 확률인데 조건이 있는 확률입니다.
조건부 확률은 다음과 같이 표기하며, 사건 F가 발생했을 때, 사건 E가 발생할 확률로 해석할 수 있습니다.
그리고 P(E l F)에서 사건 F가 조건이 됩니다. 즉, 표본 공간에서의 확률 E가 아니라, 부분 공간 F에서 사건 E가 발생할 확률을 구하는 것입니다. 그리고 수식에서 조건 F가 분모로 가고 분자는 E와 F의 교집합이 됩니다.

조건부 확률을 활용하면 P(E)는 표본 공간 S에서 E가 발생할 확률이므로 S라는 조건이 붙은 P(E l S)라고 생각해 볼 수 있습니다.
두 사건이 상호 배타(mutually exclusive)인 경우, 조건부 확률
사건 E와 사건 F가 상호 배타 인 경우 교집합이 0이 됩니다. 따라서 조건부 확률 P(E l F) = 0이 됩니다.
F가 E의 부분 집합인 경우 조건부 확률
F $\subset$ E인 경우 조건부 확률P(E l F)= 1이 됩니다. E와 F의 교집합은 F가 되기 때문입니다. 분모는 P(F)가 되어 결국 1이 됩니다.
예시 문제 1
몇 가지 예시 문제를 풀어보도록 하겠습니다.
150개 공이 들어 있는 가방에서 임의로 한개의 공을 선택하겠습니다. 150개 공은 빨강색 또는 파랑색이고, 칙칙하거나 밝습니다. 36개의 밝은 빨강색 공이 있고, 54개의 파랑색 공이 있습니다.
선택된 공이 빨강색이라는 조건에서 밝을 확률P(밝은 ㅣ 빨강색)은 어떻게 될까요?
우선 각각의 사건을 정의하는 것이 중요합니다.
P(빨강색) = 96/150
P(파랑색) = 54/150
P(밝은 빨강색) = 36/150 (빨강색과 밝은 것의 교집합 입니다.)
P(밝은 ㅣ 빨강색) = P(밝은 빨강색) / P(빨강색) 으로 정의하여 풀 수 있습니다.
예시 문제 2
동전을 두 번 던졌습니다. 표본 공간 S = {(h,h), (h,t), (t,h), (t,t)} 라고 가정하겠습니다. 첫 번째 동전이 앞면이 나온 조건에서 두 동전이 모두 앞면이 나올 조건부 확률을 구하는 문제입니다.
첫 번째 동전이 앞면이 나온 사건을 정의해보겠습니다.
F = {(h,h), (h,t)}
두 동전이 모두 앞면이 나온 사건을 정의하겠습니다.
B = {(h,h)}
이제 조건부 확률 P(B l F)를 구할 수 있습니다.
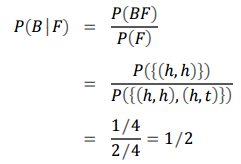
교집합을 조건부 확률로 정리하기
교집합을 조건부 확률로 정리할 수 있습니다. 교집합을 조건부 확률로 정의하여 어려운 문제를 풀 수 있게 됩니다. 어떻게 정리하는 지 알아보도록 하겠습니다.

여기서 양변에 P(F)를 곱해주면 됩니다.
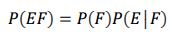
이를 활용한 예시 문제를 한번 풀어보도록 하겠습니다.
철수가 화학수업과 프랑스어 수업 중 어떤 수업을 들을지 결정하게 못했습니다. 철수는 프랑스어 수업에서 A를 받을 확률을 1/2 로 예측했고, 화학 수업에서 A를 받을 확률을 2/3 으로 예측했습니다. 그리고 철수는 수업을 동전 던지기로 결정하기로 했을 때, 화학에서 A를 받을 확률은 얼마나 될까요?
우선 각 이벤트를 정의해야 합니다.
P(A l F) = 1/2
P(A l C) = 2/3
P(C) = 1/2
P(F) = 1/2
문제에서 묻는 것은 P(CA) 이므로 다음과 같이 구할 수 있습니다.
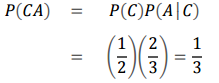
확률의 곱셈 법칙(Multiplicative Rules in Probability)
확률의 곱셈 법칙은 교집합을 조건부 확률로 나타낸 것을 n개의 사건으로 확장한 것입니다.
사건이 두 개일 때
P(AB) = P(A)P(B l A) = P(B)P(A l B)
사건이 세 개일 때
P(ABC) = P(AB)P(C l AB) = P(A)P(B l A)P(C l AB)
이처럼 n개의 사건까지 확장할 수 있습니다.

교집합을 계속 조건부확률의 곱으로 나타낸 것을 확률의 곱셈 법칙이라고 합니다.
위 계산은 각 확률이 독립이면 계산이 간단해집니다.
독립에 대해서는 다음 포스팅에서 알아보도록 하겠습니다. 감사합니다.
'수학 > 확률론' 카테고리의 다른 글
| [확률론] Odds(오즈, 아즈) (0) | 2021.01.29 |
|---|---|
| [확률론] 베이즈 정리(Bayes' Rule) (0) | 2021.01.29 |
| [확률론] 확률의 공리와 기본 성질(Axioms and Basic Properties of Probability) (4) | 2021.01.25 |
| [확률론] 집합 연산(Set Operation)과 집합 연산의 법칙(Laws of Set Operation) (1) | 2021.01.25 |
| [확률론] 표본 공간과 사건(Sample Space and Events) (0) | 2021.01.25 |